2018中考函数与几何综合的压轴题

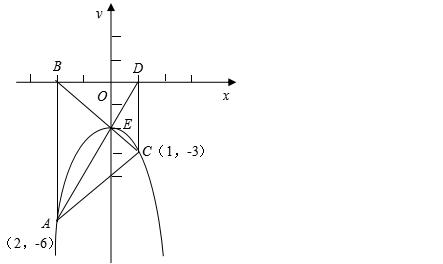
1.如图①，在平面直角坐标系中，AB、CD都垂直于x轴，垂足分别为B、D且AD与B相交于E点.已知：A(-2,-6),C(1,-3)

(1)求证：E点在y轴上；

(2)如果有一抛物线经过A，E，C三点，求此抛物线方程.

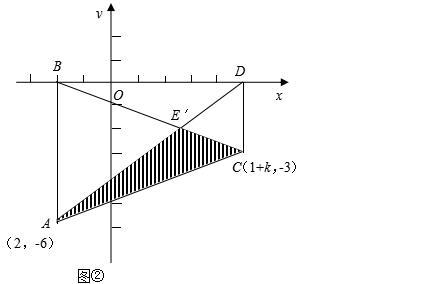
(3)如果AB位置不变，再将DC水平向右移动k(k>0)个单位，此时AD与BC相交于E′点，如图②，求△AE′C的面积S关于k的函数解析式.

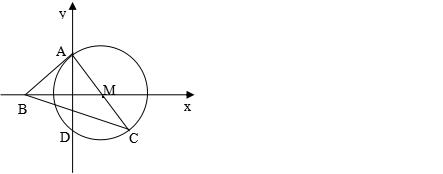
2. 已知：如图，在直线坐标系中，以点M（1，0）为圆心、直径AC为2√2的圆与y轴交于A、D两点.

（1）求点A的坐标；

（2）设过点A的直线y＝x＋b与x轴交于点B.探究：直线AB是否⊙M的切线？并对你的结论加以证明；

（3）连接BC，记△ABC的外接圆面积为S1、⊙M面积为S2，若S1/S2=h/4，抛物线y＝ax²＋bx＋c经过B、M两点，且它的顶点到x轴的距离为h,求这条抛物线的解析式.