平行四边形的两邻边之和等于平行四边形周长的一半.
例:已知,□ABCD的周长为60cm,对角线AC、BD相交于点O,△AOB的周长比△BOC的周长多8cm,求这个四边形各边长.
解:∵四边形ABCD为平行四边形
∴AB = CD,AD = CB,AO = CO
∵AB+CD+DA+CB = 60
AO+AB+OB-(OB+BC+OC) = 8
∴AB+BC = 30,AB-BC =8
∴AB = CD = 19,BC = AD = 11
答:这个四边形各边长分别为19cm、11cm、19cm、11cm.
这道题就很好的应用了这个规律,根据已知条件组成方程组,很快就得到答案。
平行四边形被对角线分成四个小三角形,相邻两个三角形周长之差等于邻边之差
有平行线时常作平行线构造平行四边形
例:已知,如图,Rt△ABC,∠ACB = 90°,CD⊥AB于D,AE平分∠CAB交CD于F,过F作FH∥AB交BC于H
求证:CE = BH
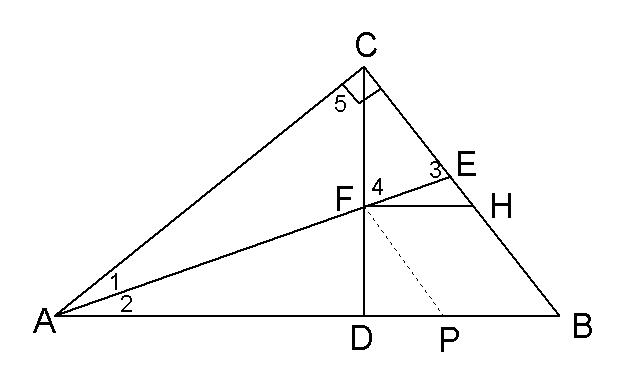
证明:过F作FP∥BC交AB于P,则四边形FPBH为平行四边形
∴∠B =∠FPA,BH = FP
∵∠ACB = 90o,CD⊥AB
∴∠5+∠CAB = 45o,∠B+∠CAB = 90o
∴∠5 =∠B
∴∠5 =∠FPA
又∵∠1 =∠2,AF = AF
∴△CAF≌△PAF
∴CF = FP
∵∠4 =∠1+∠5,∠3 =∠2+∠B
∴∠3 =∠4
∴CF = CE
∴CE = BH
根据这个规律给大家留上一道练习题,大家可以在评论里说解题方法。
练习:已知,如图,AB∥EF∥GH,BE = GC。求证:AB = EF+GH
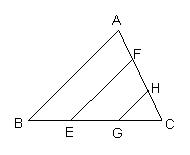
有以平行四边形一边中点为端点的线段时常延长此线段.
例:已知,如图,在□ABCD中,AB = 2BC,M为AB中点。求证:CM⊥DM
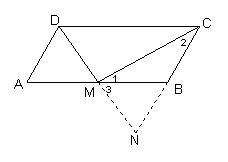
证明:延长DM、CB交于N
∵四边形ABCD为平行四边形
∴AD = BC,AD∥BC
∴∠A = ∠NBA ∠ADN =∠N
又∵AM = BM
∴△AMD≌△BMN
∴AD = BN
∴BN = BC
∵AB = 2BC,AM = BM
∴BM = BC = BN
∴∠1 =∠2,∠3 =∠N
∵∠1+∠2+∠3+∠N = 180°,
∴∠1+∠3 = 90°
∴CM⊥DM
平行四边形对角线的交点到一组对边距离相等.
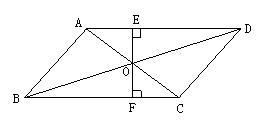
如图:OE = OF
平行四边形一边(或这边所在的直线)上的任意一点与对边的两个端点的连线所构成的三角形的面积等于平行四边形面积的一半.
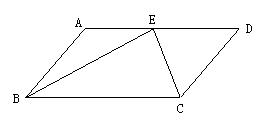
如图:S△BEC=1/2(S□ABCD)
平行四边形内任意一点与四个顶点的连线所构成的四个三角形中,不相邻的两个三角形的面积之和等于平行四边形面积的一半.
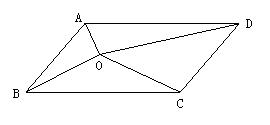
如图:
S△AOB+S△DOC= S△BOC+S△AOD =1/2(S□ABCD)
任意一点与同一平面内的矩形各点的连线中,不相邻的两条线段的平方和相等
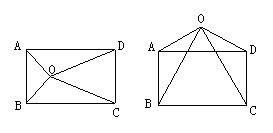
如图:AO²+OC²= BO ²+DO²
平行四边形四个内角平分线所围成的四边形为矩形
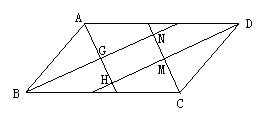
如图:四边形GHMN是矩形
上面这个规律比较简单,大家可以自己证明,我就不再给大家证明了。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论