一、选择题(每小题3分,共24分)
1.在四个实数-2,0,-√2,1 中,最大的实数是( D )
A.-2 B.0 C.-√2 D.1
2.在点(2,3),(1,0),(0,-2),(0,0),(-3,2)中,不属于任何象限的有( C )
A.1个 B.2个 C.3个 D.4个
3.以下各组数为边长,能组成直角三角形的是( B )
A.8,15,7 B.8,10,6 C.5,8,10 D.8,3,40
4.如图,在直径为 AB 的半圆 O 上有一动点 P 从点 A 出发,按顺时针方向绕半圆匀速运动到点 B,然后再以相同的速度沿着直径回到点 A 停止,线段 OP 的长度 d 与运动时间 t 之间的函数关系用图象描述大致是( A )

5.设 n 为正整数,且 n< √65 < n+1,则 n 的值为( D )
A.5 B.6 C.7 D.8
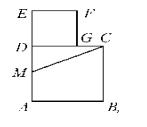
6.如图,在边长为 2 的正方形 ABCD 中,点 M 为边 AD 的中点,延长 MD 至点 E,使
ME=MC,以 DE 为边作正方形 DEFG,点 G 在边 CD 上,则 DG 的长为( D )
A.√3-1 B.3-√5 C.√5+1 D.√5-1
7.在全民健身环城越野赛中,甲乙两选手的行程 y (千米) 随时间 x (时) 变化的图象(全程)如图所示.有下列说法:
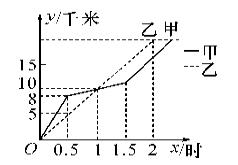
① 起跑后1小时内,甲在乙的前面;
② 第1小时两人都跑了10千米;
③ 甲比乙先到达终点;
④ 两人都跑了20千米.其中正确的说法有( C )
A.1个 B.2个 C.3个 D.4个
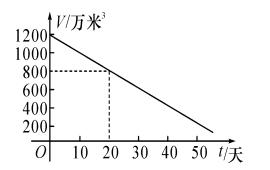
8.由于干旱,某水库的蓄水量随时间的增加而直线下降.若该水库的蓄水量 V (万立方米)与干旱的时间 t (天)的关系如图所示,则下列说法正确的是( A )
A.干旱开始后,蓄水量每天减少 20 万立方米
B.干旱开始后,蓄水量每天增加 20 万立方米
C.干旱开始时,蓄水量为200 万立方米
D.干旱第 50 天时,蓄水量为1200 万立方米
二、填空题(每小题3分,共24分)
9.如果正比例函数 y=kx 的图象经过点 (1,-2),那么k的值等于__-2__.
10.在 △ABC 中,∠C=90°,AB=7,BC=5,则边 AC 的长为__2√6__.
11.已知点 A(a,5) 与 B(2,b) 关于 y 轴对称,则 a+b=__3__.
12.计算:27的立方根-|-2|=__1__.
13.已知 P1(1,y1),P2(2,y2) 是正比例函数 y=1/3 x 的图象上的两点,则 y1__<__y2.(填“>”“<”或“=”)
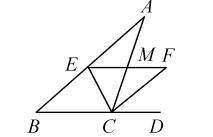
14.如图,在 △ABC 中,CE 平分 ∠ACB,CF 平分 △ABC 的外角 ∠ACD,且 EF∥BC 交 AC 于点 M,若 EF=5,则 CE^2+CF^2=__25__.
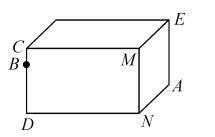
15.如图所示,一块砖宽 AN=5 cm,长 ND=10 cm,CD 上的点 B 距地面的高 BD=8 cm,地面上的点 A 处的一只蚂蚁到点 B 处吃食,要爬行的最短路线是__17__cm.
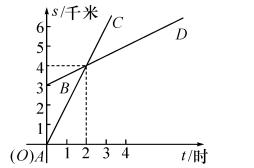
16.如图,已知 A 地在 B 地正南方 3 千米处,甲乙两人同时分别从 A,B 两地向正北方向匀速直行,他们与 A 地的距离 s(千米) 与所行的时间 t(小时) 之间的函数关系图象用如图所示的AC 和 BD 表示,当他们行走 3 小时后,他们之间的距离为__1.5__千米.
三、解答题(共72分)
17.(8分)计算:
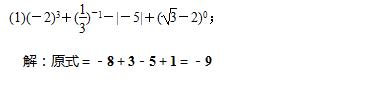
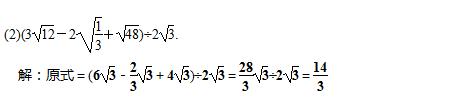
18.(8分)有6个实数:
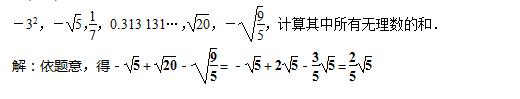
19.(8分)实数 a,b 在数轴上的位置如图所示,
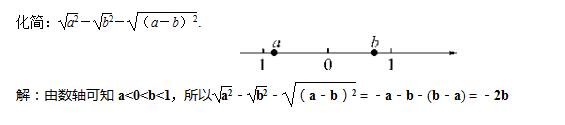
20.(8分)如图所示,一次函数的图象与 x 轴,y 轴交于点 A,B,如果点 A 的坐标为
(4,0),且 OA=2OB,求一次函数的表达式.
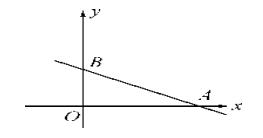

21.(8分)在平面直角坐标系中,已知点 A(0,2),点 B(0,-3),三角形 ABC 的面积为 5,点 C 到 x 轴的距离为 2,求点 C 的坐标.
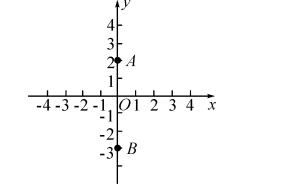
解:C(2,2)或C(-2,2)或C(2,-2)或(-2,-2)
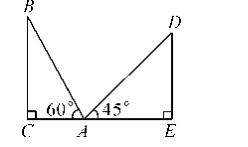
22.(10分)如图,在两面墙之间有一个底端在点 A 的梯子,当它靠在一侧墙上时,梯子的顶端在点 B;当它靠在另一侧墙上时,梯子的顶端在点 D,已知∠BAC=60°,∠DAE=45°,点D 到地面的垂直距离 DE=3√2 m,求点 B 到地面的垂直距离 BC.

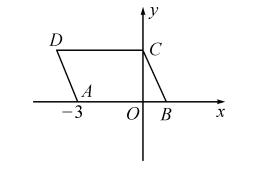
23.(10分)如图所示,平行四边形 ABCD 的边长 AB=4,BC=2.若把它放在平面直角坐标系中,使 AB 在 x 轴上,点 C 在 y 轴上,如果点A的坐标为(-3,0),求点B,C,D的坐标.

24.(12分)某天,小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.图中线段 AB,OB 分别表示父子俩送票、取票过程中,离体育馆的路程 s(米) 与所用时间 t(分) 之间的函数关系,结合图象解答下列问题:(假设骑自行车和步行的速度始终保持不变)
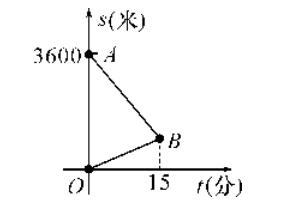
(1)求点B的坐标和AB所在直线的函数关系式;
(2)小明能否在比赛开始前到达体育馆?



 加载中,请稍侯......
加载中,请稍侯......
精彩评论