大家好,今天和大家分享矩形和直角三角形的规律和应用。
有垂直时可作垂线构造矩形或平行线.
例:已知,如图,E为矩形ABCD的边AD上一点,且BE = ED,P为对角线BD上一点,PF⊥BE于F,PG⊥AD于G
求证:PF+PG = AB
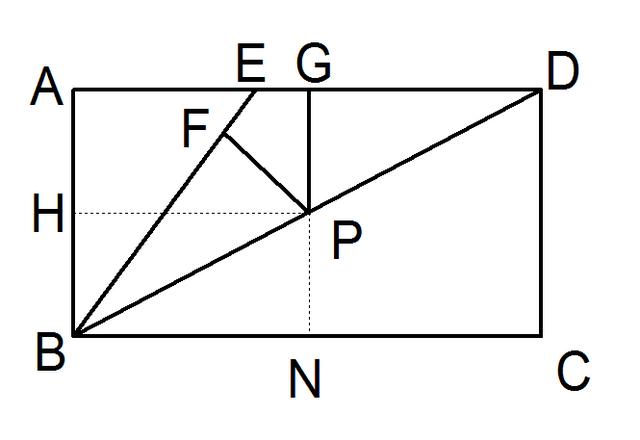
证明:过P作PH⊥AB于H,则四边形AHPG为矩形
∴AH = GP PH∥AD
∴∠ADB =∠HPB
∵BE = DE
∴∠EBD = ∠ADB
∴∠HPB =∠EBD
又∵∠PFB =∠BHP = 90o
∴△PFB≌△BHP
∴HB = FP
∴AH+HB = PG+PF
即AB = PG+PF
这道题的第二种证明方法,可以延长GP交BC于N,则四边形ABNG为矩形,不再证明!
直角三角形常用辅助线方法
作斜边上的高
例:已知,如图,若从矩形ABCD的顶点C作对角线BD的垂线与∠BAD的平分线交于点E
求证:AC = CE
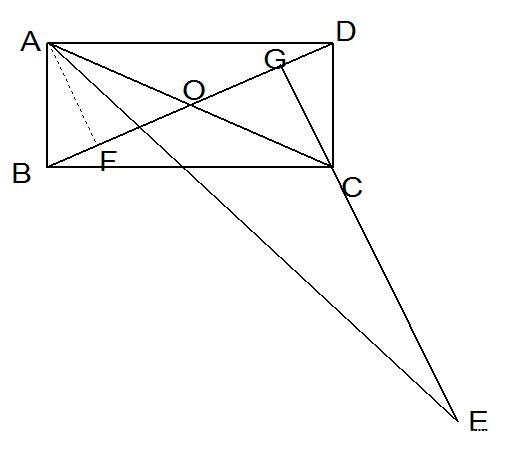
证明:过A作AF⊥BD,垂足为F,则AF∥EG
∴∠FAE = ∠AEG
∵四边形ABCD为矩形
∴∠BAD = 90° OA = OD
∴∠BDA =∠CAD
∵AF⊥BD
∴∠ABD+∠ADB = ∠ABD+∠BAF = 90°
∴∠BAF =∠ADB =∠CAD
∵AE为∠BAD的平分线
∴∠BAE =∠DAE
∴∠BAE-∠BAF =∠DAE-∠DAC
即∠FAE =∠CAE
∴∠CAE =∠AEG
∴AC = EC
作斜边中线,当有下列情况时常作斜边中线
①有斜边中点时
例:已知,如图,AD、BE是△ABC的高, F是DE的中点,G是AB的中点
求证:GF⊥DE
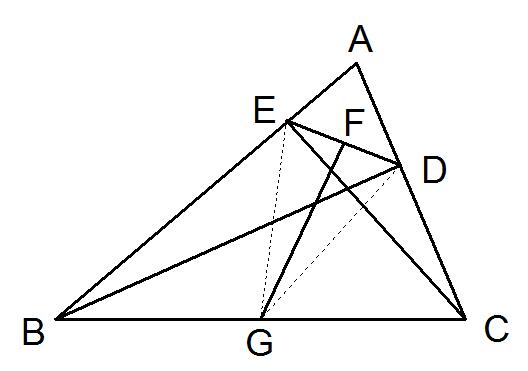
证明:连结GE、GD
∵AD、BE是△ABC的高,G是AB的中点
∴GE =1/2AB,GD =1/2AB
∴GE = GD
∵F是DE的中点
∴GF⊥DE
②有和斜边倍分关系的线段时
例:已知,如图,在△ABC中,D是BC延长线上一点,且DA⊥BA于A,AC =1/2BD
求证:∠ACB = 2∠B
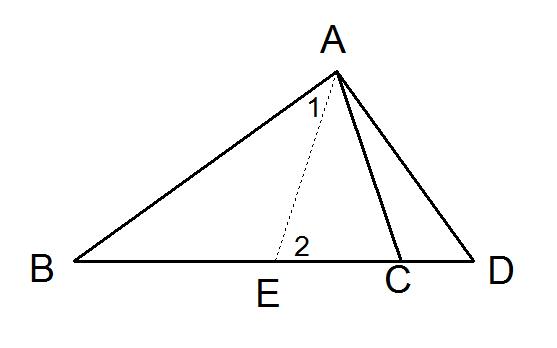
证明:取BD中点E,连结AE,则AE = BE =1/2BD
∴∠1 =∠B
∵AC =1/2BD
∴AC = AE
∴∠ACB =∠2
∵∠2 =∠1+∠B
∴∠2 = 2∠B
∴∠ACB = 2∠B
有线段中点时,常过中点作平行线,利用平行线等分线段定理的推论证题
例:已知:△ABC中,D为AB中点,E为BC的三等分点,(BE>CE)AE、CD交于点F
求证:F为CD的中点
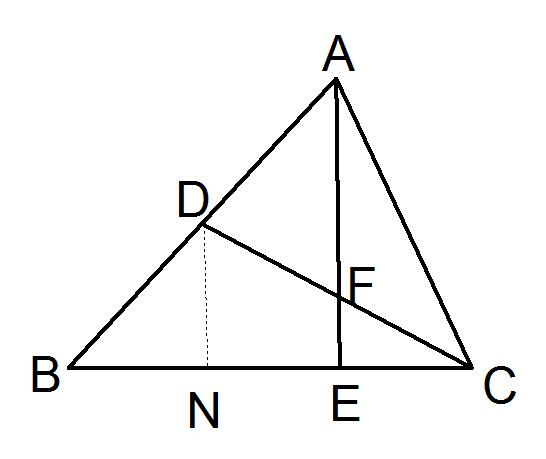
证明:过D作DN∥AE交BC于N
∵D为AB中点
∴BN = EN
又∵E为BC的三等分点
∴BN = EN = CE
∵DN∥AE
∴F为CD的中点
正方形一条对角线上一点到另一条对角线上的两端距离相等
例:已知,如图,过正方形ABCD对角线BD上一点P,作PE⊥BC于E,作PF⊥CD于F, 求证:AP = EF
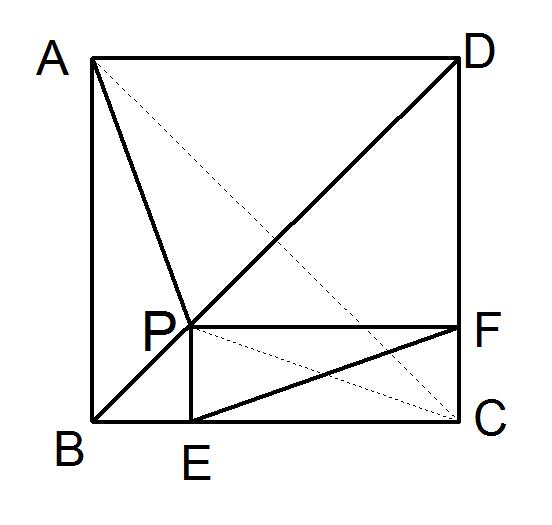
证明:连结AC 、PC
∵四边形ABCD为正方形
∴BD垂直平分AC,∠BCD = 90°
∴AP = CP
∵PE⊥BC,PF⊥CD,∠BCD = 90°
∴四边形PECF为矩形
∴PC = EF
∴AP = EF
有正方形一边中点时常取另一边中点
例:已知,如图,正方形ABCD中,M为AB的中点,MN⊥MD,BN平分∠CBE并交MN于N
求证:MD = MN
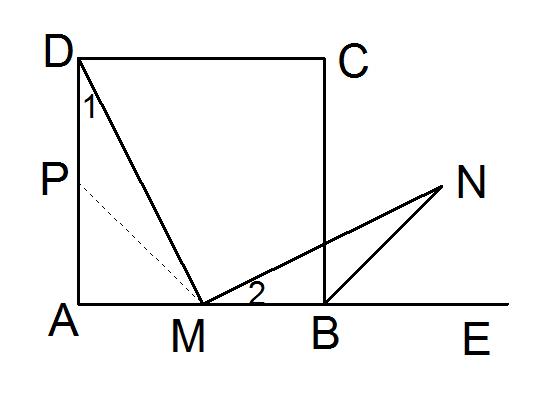
证明:取AD的中点P,连结PM,则DP = PA =1/2AD
∵四边形ABCD为正方形
∴AD = AB, ∠A =∠ABC = 90°
∴∠1+∠AMD = 90°,又DM⊥MN
∴∠2+∠AMD = 90°
∴∠1 =∠2
∵M为AB中点
∴AM = MB =1/2AB
∴DP = MB AP = AM
∴∠APM =∠AMP = 45°
∴∠DPM =135°
∵BN平分∠CBE
∴∠CBN = 45°
∴∠MBN =∠MBC+∠CBN = 90°+45°= 135°
即∠DPM =∠MBN
∴△DPM≌△MBN
∴DM = MN
注意:把M改为AB上任一点,其它条件不变,结论仍然成立。
下面给大家留一道练习题,欢迎大家踊跃留言,说出自己的方法:
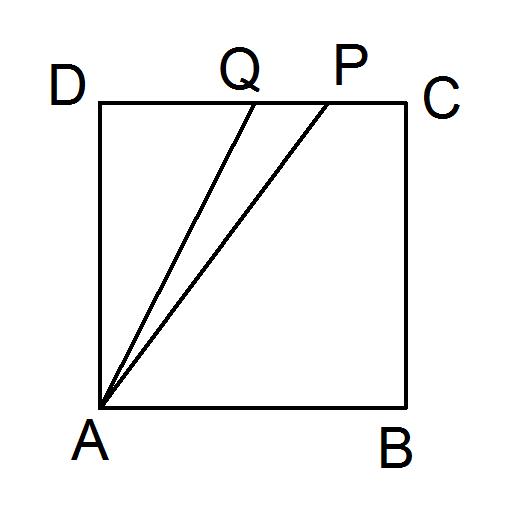
练习:已知,Q为正方形ABCD的CD边的中点,P为CQ上一点,且AP = PC+BC
求证:∠BAP = 2∠QAD

 加载中,请稍侯......
加载中,请稍侯......
精彩评论