面积问题是中考考试中的一个系列，总体难度有点大，今天我就总结一下由动点产生的面积问题。搞懂这几个题目，中考压轴题中碰到再也不会害怕了。
例1： 本题主要考查了二次函数综合题，此题涉及到了待定系数法求二次函数的解析式、二次函数的性质、比例的性质以及一元二次方程的解法。解答本题的关键求出点B的坐标。
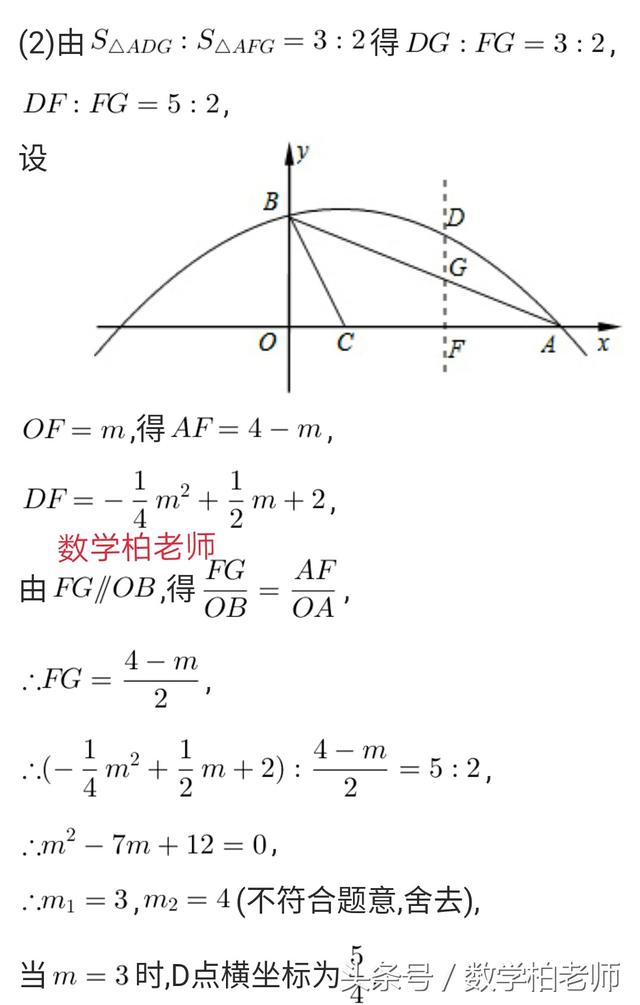
所以点D的坐标为（3，5 /4）
例2：此题属于二次函数综合题，涉及的知识有：待定系数法确定二次函数解析式，待定系数法确定一次函数解析式，直角梯形的判定，直线与二次函数的交点，坐标与图形性质，熟练掌握待定系数法是解本题的关键。
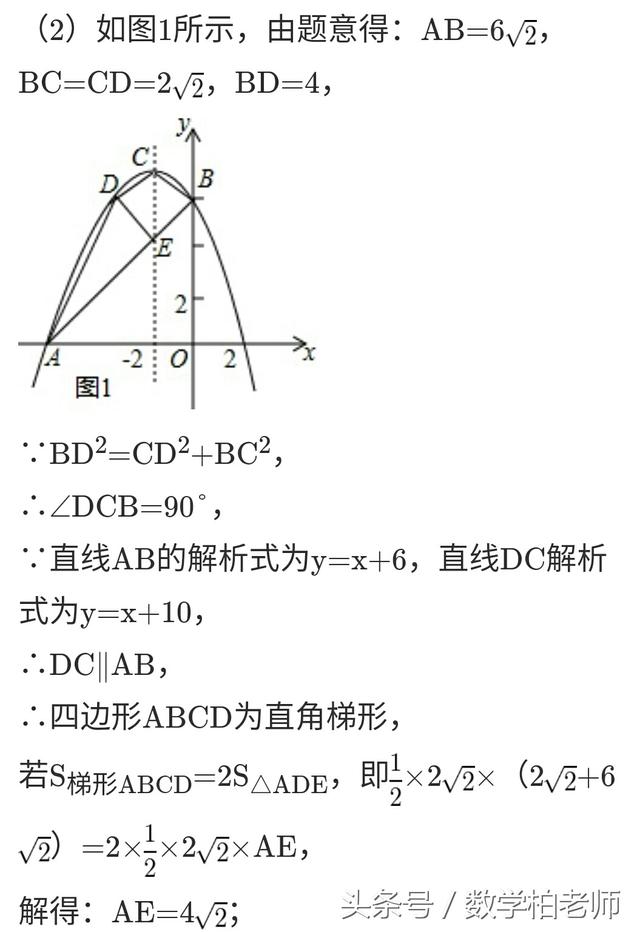
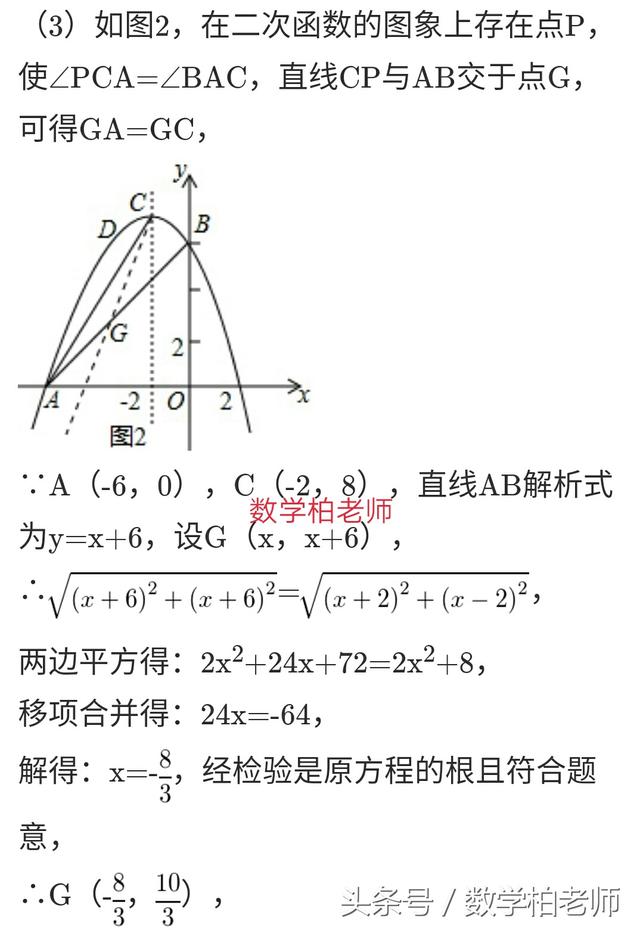
例3：衡阳市中考试题：
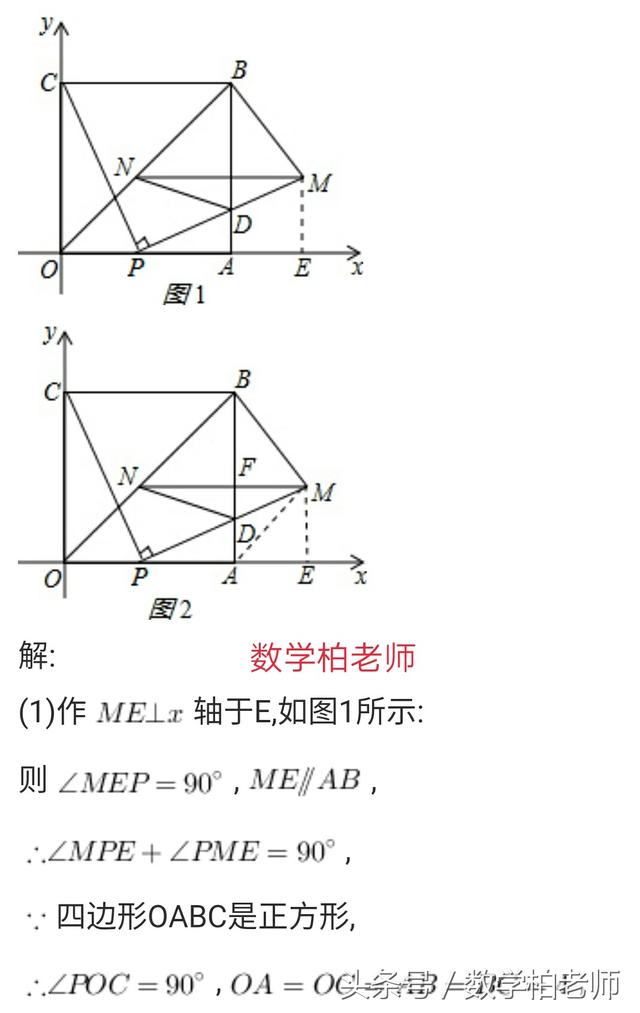
加载中,请稍侯......
精彩评论