二次函数压轴题6，求动线段长度的最大值及等腰三角形存在性问题

【题目呈现】

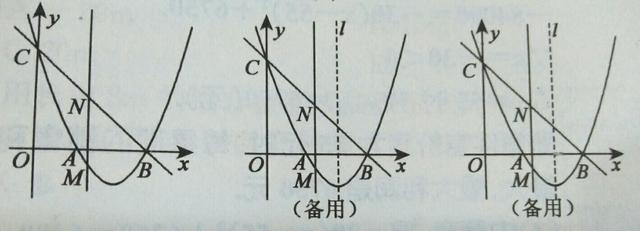
如下图，抛物线y=X²+bx十C与X轴交于点A和点B(3，0)，与y轴交于点C(0，3).

(1)求抛物线的解析式;

(2)若点M是抛物线上在x轴下方的动点，过点M作MN∥y轴交直线BC于点N，求线段MN的最大值;

(3)在(2)的条件下，当MN取最大值时，在抛物线的对称轴L上是否存在点P，使△PBN是等腰三角形？若存在，请直接写出所有点P的坐标;若不存在，请说明理由.

【分析】

(1)用待定系数法即可求解;

(2)求出直线BC的解析式，由于MN∥y轴，点M，点N的横坐标相同，纵坐标用相应的函数关系式表示，进而求出线段MN的关系式，即可求最大值;

(3)等腰三角形存在性问题，当有两定点，一动点时，一般用线段两两相等分类讨论，具体写的时侯，用线段的平方两两相等;当有一定点，两动点时往往用三线合一性质比较简便。

【答案与解析】

解:(1)∵抛物线y=x²+bx十C过点B(3，0)与点C(0，3)，∴可得①3²十3b十C=0，②0²+0b十C=3，∴C=3，b=一4，∴抛物线的解析式为y=x²一4x+3.

(2)令x²一4x+3=0，则X1=1，x2=3，∴A点坐标为(1，0)，设直线BC的解析式为y=Kx+b(K、b为常数且K≠0)，∵点B(3，0)，点C(0，3)在直线BC上，∴可得:

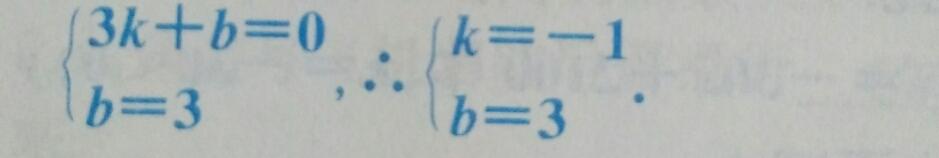
∴直线BC的解析式为y=一x十3，由于MN∥y轴，M在抛物线上x轴下方，N在BC上，所以设N(x，一x十3)，则M(x，x²一4X十3)(1<x<3)，MN=(一x十3)一(x²一4X+3)=一x²+3x=一(x一3/2)²十9/4，∴当x=3/2时，MN的最大值为9/4.

(3)由y=x²一4x十3=0，可得对称轴为直线x=2，在②的条件下N点坐标为(3/2，3/2)，由于点P在对称轴上，所以设P点坐标为(2，y)，又B点为(3，0)，PN²=(2一3/2)²+(y一3/2)²=y²一3y十5/2，PB²=(2一3)²+y²=y²+1，NB²=(3一3/2)²+(0一3/2)²=9/2，

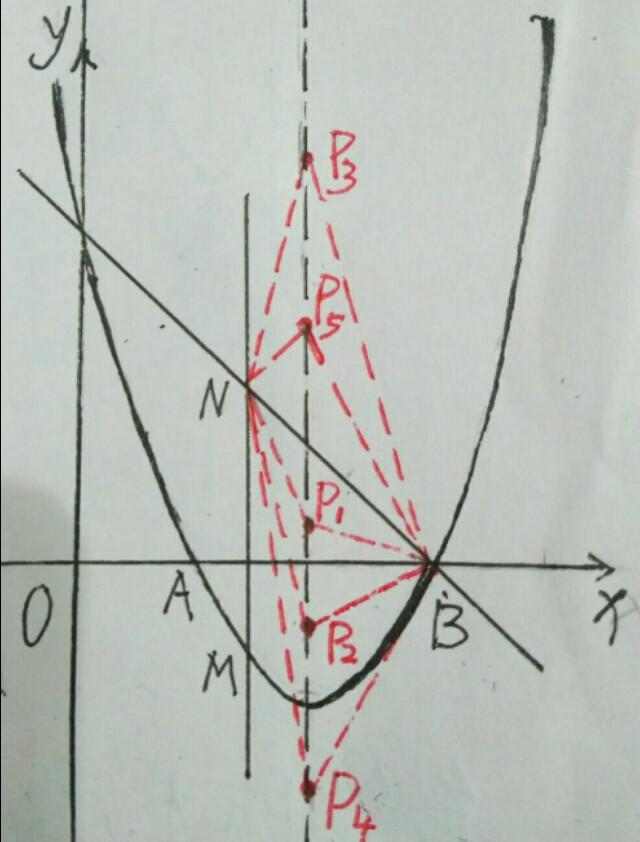
①当PN=PB，即PN²=PB²时，y²一3y十5/2=y²+1，解得y=1/2，此时记点P1(2，1/2)如下图;

②当PN=NB，即PN²=NB²时，y²一3y十5/2=9/2，解得y1=3/2十√17/2，y2=3/2一√17/2，此时记点P为P2(2，3/2一√17/2)，P3(2，3/2+√17/2);

③当PB=NB，即PB²=NB²时，y²十1=9/2，解得y=±√14/2，此时记点P为P4(2，一√14/2)，P5(2，√14/2).

综上所述，符合条件的所有P点为(2，1/2)或(2，3/2一√17/2)或(2，3/2十√17/2)或(2，一√14/2)或(2，√14/2).

【反思】

熟练掌握，线段长度的表示方法及分类讨论的思想。