谈谈等腰三角形的存在性问题

 等腰三角形的存在性问题一直是近年中考热点之一，常出现在综合题中，属于难度大知识点覆盖面广的一种题型，常用的解决方法有以下三种：

方法一：几何法“两圆一线”

如下图，已知点A、B和直线l，在l上是否存在点P，使以A、B、P为顶点的三角形是等腰三角形，若存在，有几个符合条件的点P？

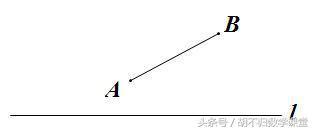
方法：分别以点A、B为圆心，以线段AB长为半径作圆，然后作AB的中垂线，两圆和中垂线与l的所有交点即为P点，共5个，如下图所示：

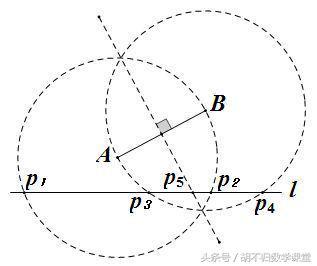
方法二：“分情况讨论法”

题中给出的条件不明确，哪个是三角形的腰无法确定，这时要分不同情况求解，表示出三角形三个顶点A、B、P的坐标，再表示出线段AB、BP、AP的长度，分三种情况讨论：①AB＝AP；②BA＝BP；③PB＝PA，分别列方程解出坐标。

方法三：作等腰三角形底边的高，用勾股定理或相似建立等量关系求解。

☞在实战中，找点的位置和个数适合用第一种“两圆一线”法，第二、三种方法更适合求点的坐标。

我们来研究今年山西的一道中考题：

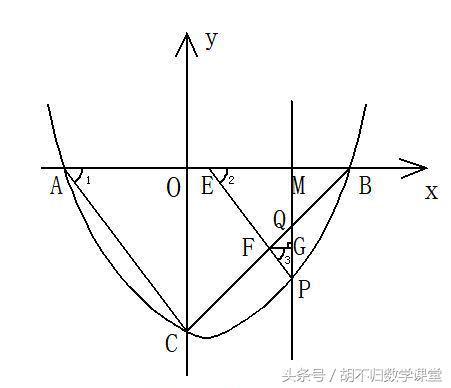
（ 1） 求 A、 B 、C 三点的坐标；

（ 2） 试探究在点 P 的 运 动 的 过 程 中，是 否 存 在 这 样 的 点 Q，使 得 以 A ，C ，Q 为 顶 点 的 三 角 形是等腰三角形 .若 存 在，请直接写出此时点 Q 的 坐 标； 若 不 存 在，请 说明理由.

解析：

第一问令y=0，求出方程的两个根，即可得到A、B的横坐标，进而可求得点A、B的坐标，令x=0，得y=-4，即可得到C点的坐标，答案为：A(-3,0)，B（ 4，0），C（ 0， -4）.

第二问求点的坐标，不妨选择“分情况讨论法”，解答如下：

依题意分3种情况求解：

反思：“分情况讨论法”的解答过程中，要经常用到勾股定理，甚至是两点间距离公式，提醒大家注意。

下面再举几个例子：

【典例1】在平面直角坐标系中，如下图，O为原点，已知A（2，-1），P是x轴上的一个动点，如果以P，O，A为顶点的三角形是等腰三角形，那么符合条件的动点P的个数为( )

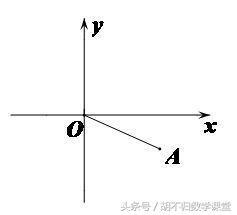
A.2 B.3 C.4 D.5

解析：求点的个数就用“两圆一线”法，很容易得到答案，如下图所示，符合要求的P点共有5个。

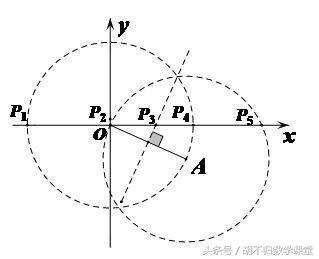
反思：等腰三角形存在性问题，根据点的特征又可分为“两定一动型”和“两动一定型”，“分情况讨论法”是通用的一种求解方法，而“两圆一线”更适用于“两定一动型”的求交点位置或个数的问题。

【典例2】如下图，已知△ABC中，∠C=90°，AC=3，BC=4，P、Q分别为AB、BC上的动点，PB=CQ=x。求：当x为何值时，△PBQ为等腰三角形？

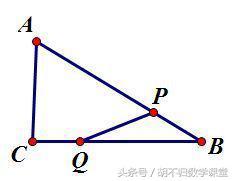
解析：本题是两个动点（P和Q）一个定点（B），需分3种情况讨论：

① 当BP=BQ时，易得4-x=x x=2.

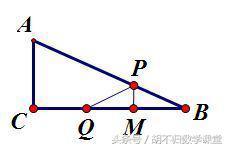
② 当PQ=PB时，如下图，过点P作PM⊥BC于点M，易证△BPM∽△BAC，再由相似比可算出答案。

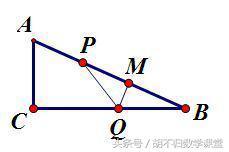
③当QP=QB时，如下图，则由△BQM∽△BAC可得答案。

反思：当有两个点是动点，一个是定点时，需要分3种情况讨论，此时一般考虑后两种方法，而作等腰三角形底边的高，由 “三线合一”走相似路线一般很好使。

☞☞求解点的坐标过程中，往往要用到勾股定理或者两点间距离公式，甚至要用上“若两直线垂直则斜率的积为-1” 得到答案 ，而这些知识课本上是没有的，其实中考最后的压轴题一般不需要过程，只需求出正确的答案即可，因此，如果作为学有余力的同学，可以拓宽视野，适当掌握一些有用的公式，也是必要的。

以下是坐标系背景下的求解题可能用得上的3个公式，供参考：

① 线段的中点坐标公式：如果线段AB的两个端点坐标分别为 （x₁,y₁）,(x₂,y₂) ，中点M的坐标记作（x, y）,则x =1/2(x₁＋x₂)，y =1/2(y₁＋y₂) 即线段的中点坐标等于它的两个端点坐标之和的一半；

②若直线y₁=k₁x＋b₁与直线y₂＝k₂x＋b₂互相垂直，则有k₁·k₂=－1；

③两点间距离公式：

设A（x₁,y₁）,B(x₂,y₂)是平面直角坐标系中的两个点,则

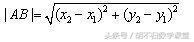
【精品练习题】

1、如下图，在长方形ABCD中，AB=4，AD=10，点Q是BC的中点，点P在AD边上运动，若△BPQ是腰长为5的等腰三角形，则满足题意的点P有( )

A.2个 B.3个 C.4个 D.5个

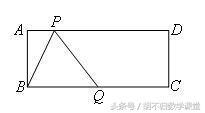
2、已知：如下图，线段AB的端点A在直线l上，AB与l的夹角为60°，请在直线l上另找一点C，使△ABC是等腰三角形．这样的点有( )

A.1个 B.2个 C.3个 D.4个

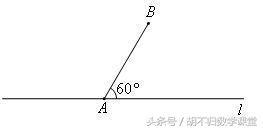
3、如下图，在△ABC中，∠ABC=90°，AB=3cm，BC=4cm．动点Q从点A出发沿AC向终点C匀速运动，速度2cm/s；同时，点P从点B出发沿BA向终点A匀速运动，速度1cm/s.

求当t为何值时，△APQ为等腰三角形？

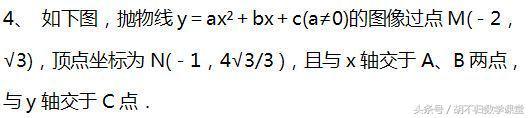
(1)求抛物线的解析式；

(2)点P为抛物线对称轴上的动点，当△PBC为等腰三角形时，求点P的坐标。

【答案】

1、B

2、B（注意：特殊三角形作两圆一线时，有些点是重合的）

3、当t为1s或9/8s或15/17s时，△APQ为等腰三角形.

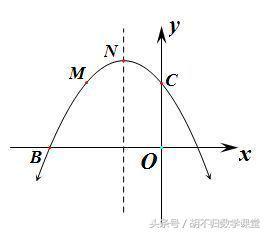
（2）方法一：分别以点B、C为圆心，线段BC长为半径作圆，交对称轴于点P2、P3、P4、P5，再作BC的垂直平分线交对称轴于点P1，故符合要求的P点共5个，利用勾股定理及已知的B和C坐标，可求出P2、P3、P4、P5，求P1时需用中点坐标公式，以及两直线垂直其斜率的积为－1求得。

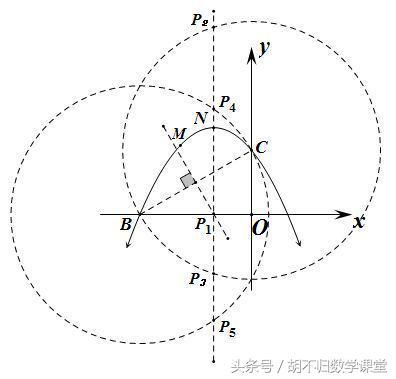
方法二：通过二次函数解析式求出点B、C的坐标；然后利用勾股定理求得线段BC的长，当△PBC为等腰三角形时，需分PB＝PC，CP＝CB，BP＝BC三种情况讨论，得到答案。

综上，当△PBC为等腰三角形时，点P的坐标为(－1，0)或(－1，√3＋√11)或(－1，√3－√11)或(－1，2√2)或(－1，－2√2 )