「初中数学」梯形+角等——转化为全等或相似

梯形+角等转化成全等或相似三角形

题目

在梯形ABCD中，AD//BC，AB=CD，BD=BC，点E在对角线BD上，

且∠DCE=∠DBC.

(1)求证：AD=BE；

(2) 延长CE交AB于点F，如果CF⊥AB，求证：4EF·FC=DE·BD

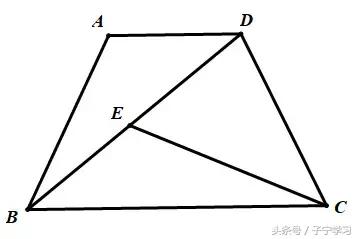
01证明线段相等，优先考虑全等

角等转化全等

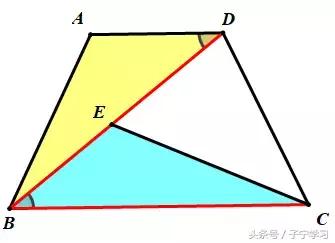
已有一边和一角两个条件，还差一个条件。

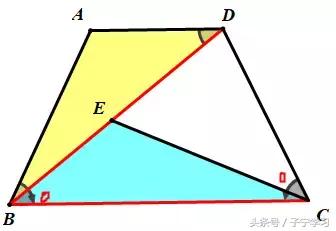
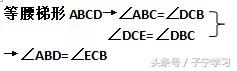
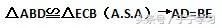
证明比例线段，考虑相似

02

分析：EF、FC所在三角形

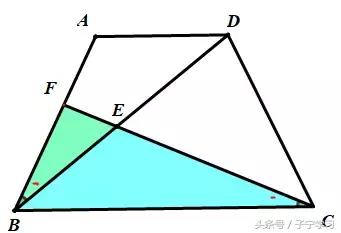
斜A相似，发现吗？

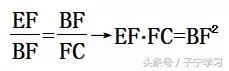
同样的分析：DE、BD所在三角形

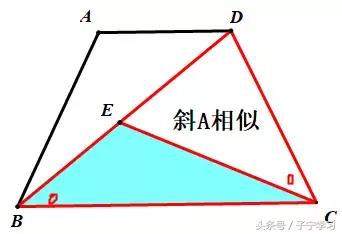
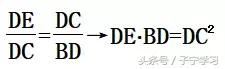
斜A相似大法

联结AC

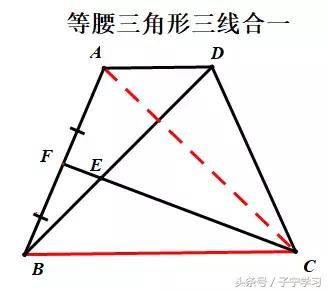
2BF=AB=CD.等量代换即可。

小结

如何证明比例式中的2倍或4倍，往往利用中点的条件进行转化，问题就解决了。

题目

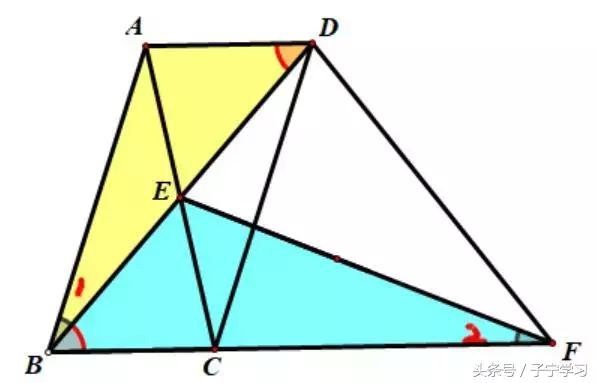
本题由上题的角转化全等→角转化相似：：△ABD∽△EBF

以上两题图形特征：梯形为背景角相等转化成全等或相似

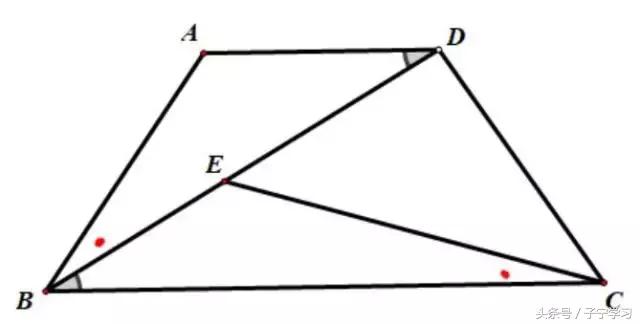
变化1：BD=BC

当BD=BC时，相似就转化为全等。

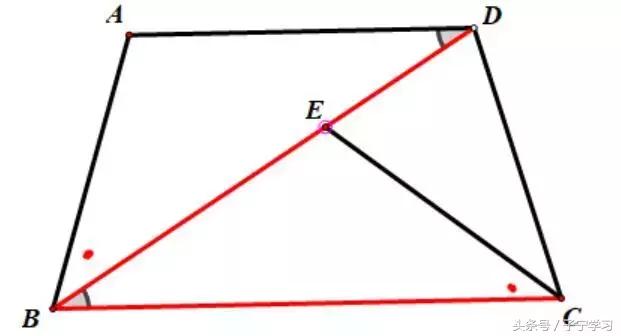
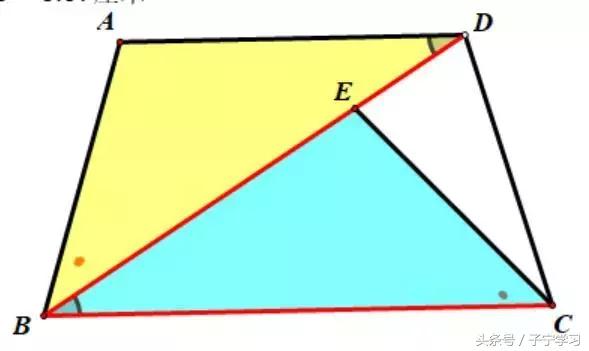
变化2：AB=DC

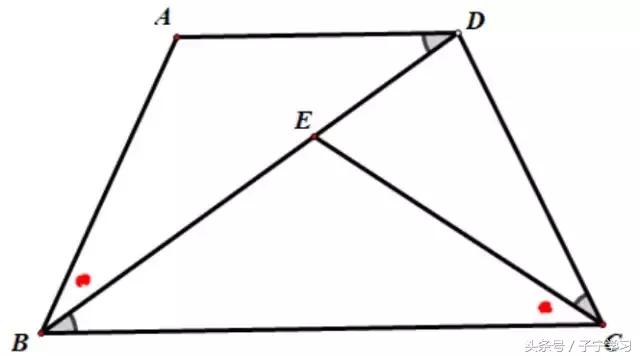
增加AB=DC条件，多了斜A相似。

链接

变式[1]一一起点

（1）同第一题一样哦

变式[2]一一进化

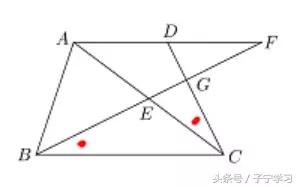
基本图形：

梯形+相等的角转化为相似（全等）

总结：两道证明题都涉及基本模型，以梯形为背景通过角相等得出全等或相似，为第二小题构建角或边的关系创造条件，在综合题中利用这个图形为后面题目的展开铺设了必不可少的基石，认识这个图形，了解题目变化规律能大大开阔解题思路。