三角形全等证明，10道考试真题，6种常用辅助线添加的方法和技巧

cc518学习网精品学习资料总目录

以下六种常用的辅助线添加方法和技巧。相互学习，一起进步。

方法一、双垂直构造三角形全等。遇见角平分线，角平分线上的点向角两边做垂直，必出三角形全等。例题1，是最基础，最简单的题型。

有些，需要我们证明角平分线的时候，同样可以向角两边做垂直，那么只要两个垂线段相等，到角两边距离相等的点在角平分线上。

例题2，过点P做MN平行BC，则出现在AB边和CD边上，双垂直。

根据题意，证明三角形QNP全等于三角形PMB，结论得证。

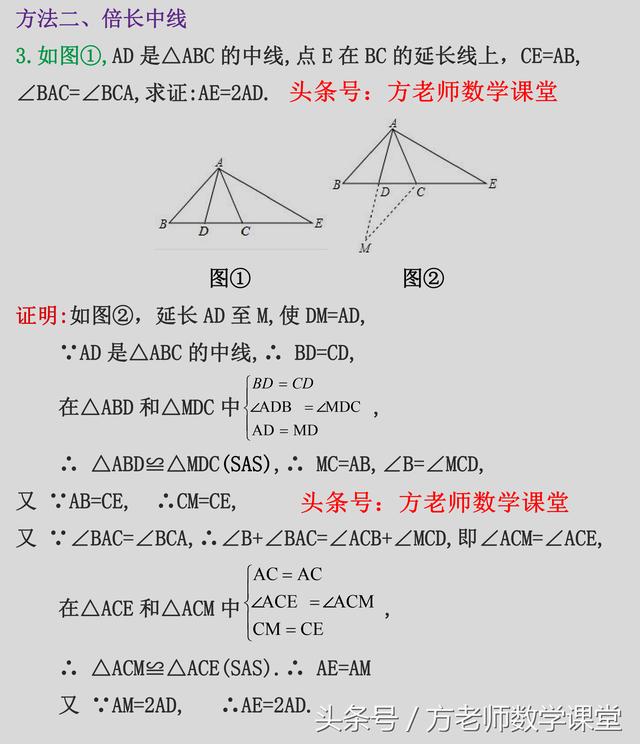
方法二，倍长中线。三角形中，遇见中点，很容易想到倍长中线。

例题3，倍长中线后，得出三角形ACE全等于三角形ACM。

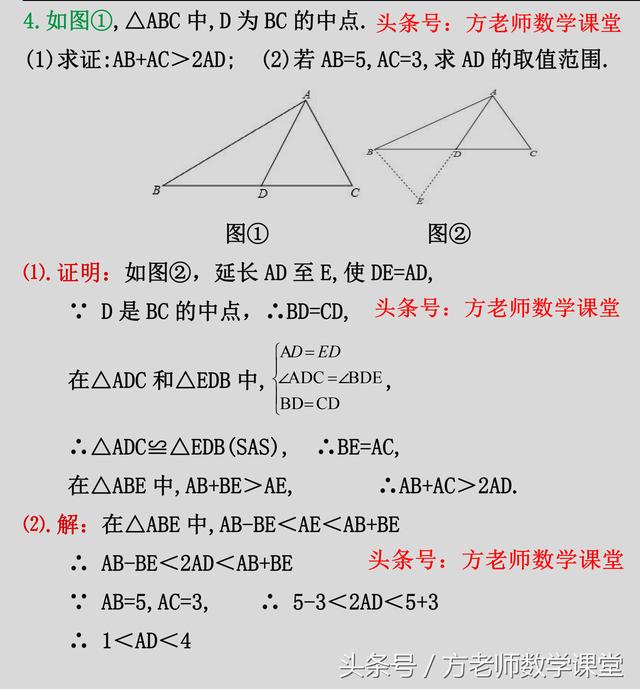
例题4，延长AD至E，使DE=AD。得出三角形ADC全等于三角形EDB。

第2小题，根据三角形的三边关系，等量代换，即可求出AD的取值范围。

方法三、截长补短法。求证两个线段和等于一个线段的时候，很容易想到截长补短的辅助线添加方法。

截长补短法，包括了截长法和补短法，两种方法。一般来说，一道题，既可以用截长法，也可以用补短法。

例题6、解析中用了延长AD至M，使MD=FD。请认真看解答过程。

再请按照图3的辅助线，自行练习推理，举一反三，得出结论。

方法四、平行线发或者平移法。解题方法1，过点O做OD平行BC。

还有两个方法，请自行推理，如图3和图4.

方法五，旋转法。把一个三角形，经过旋转，旋转后必出三角形全等，得出结论。

例8和例9，其实也就是，最近经典的半角模型。之前也专门讲过，这个几何模型。

请认真参考，这个两个例题。从中总结规律和解题方法。

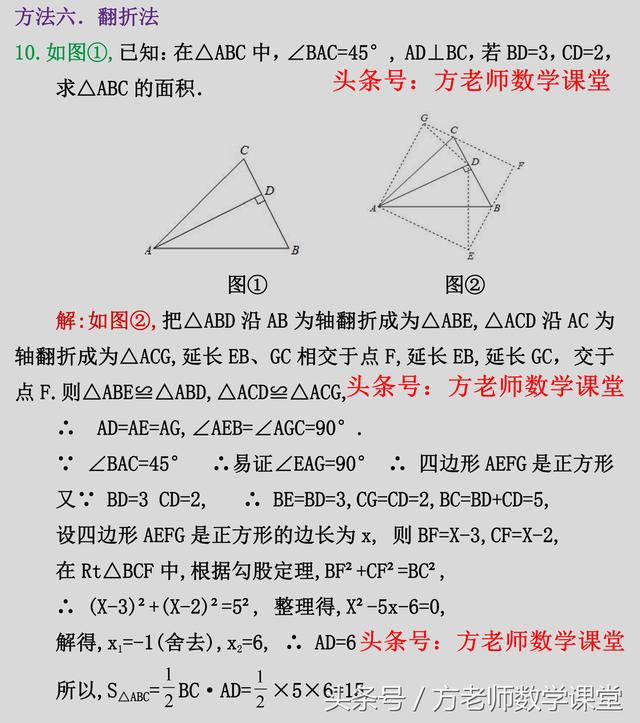
方法六、翻折法，或者叫对称法。例题10，看起来很难，当你认真看完解题过程，肯定会有所收获。