在直角坐标系中求三角形的面积，学会两种辅助方法，你就是学霸

同学们都知道二次函数是初中数学的难点，更是中考的考点，这样的拉分题当然是每年必考。有一类题型——在直角坐标系中求三角形的面积，好多同学也是束手无策，不知从何下手，今天老师告诉你们，两种方法掌握了，以后碰到此类题型，将就手到擒拿，拉分题瞬间变成送分题。

在直角坐标系中求三角形面积的两种常用方法:

(1) 补图法

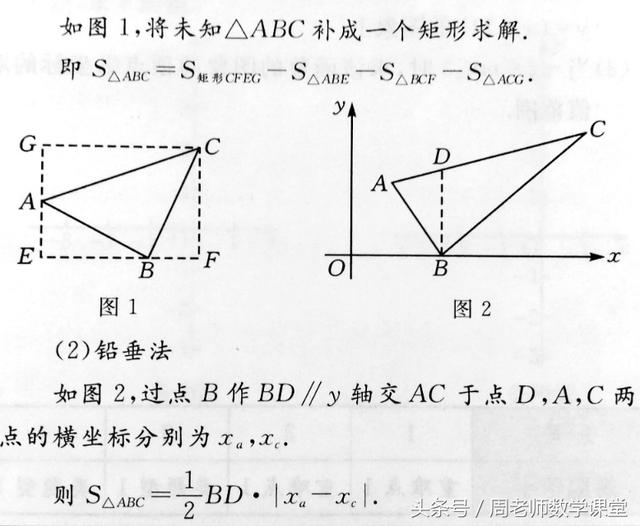
下面我用铅垂法举例说明

[解析提示]

（1）把M点坐标代入抛物线解析式可得到b与a的关系，可用a表示出抛物线解析式，化为顶点式可求得其顶点坐标；

（ll)由直线解析式可先求得m的值，联立直线与抛物线解析式，消去y，可得到关于x的一元二次方程，再判断其判别式大于0即可；

(lll)(i) 由（ll)的方程，可求得N点坐标，利用勾股定理可求得MN2，利用二次函数性质可求得MN长度的取值范围；

（ii）设抛物线对称轴交直线与点E，则可求得E点坐标，利用S△QMN=S△QEN+S△QEM可用a表示出△QMN的面积，再整理成关于a的一元二次方程，利用判别式可得其面积的取值围，可求得答案。

[解题步骤]

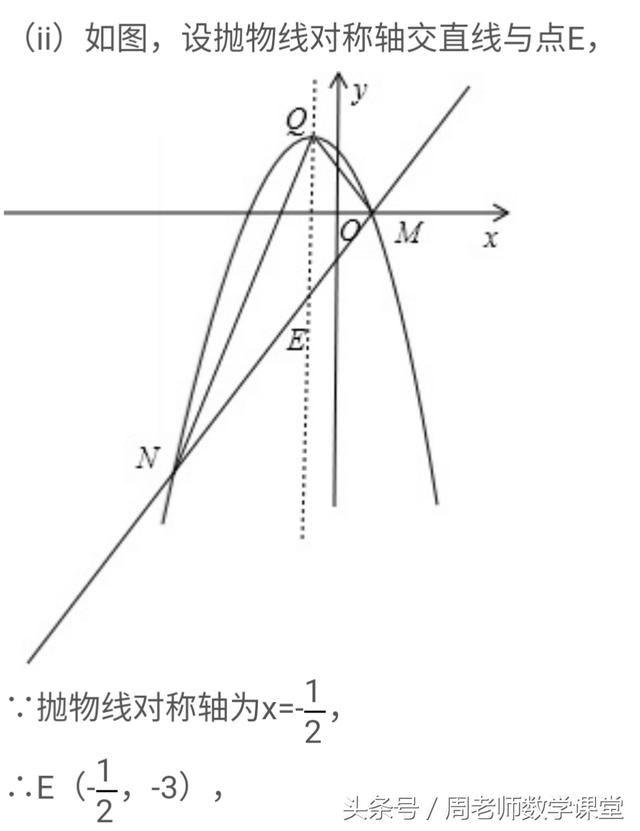
上题最后一问就是用铅垂法，列出三角形的面积公式，最后用a表示三角形的面积，解a的一元二次方程，通过判别式求面积的最小值，不知你看懂了吗？

欢迎留言，评论，关注。