三角形从入门到提高，看了这篇就够了

首先我们从两张图来认识三角形和它的相关概念。

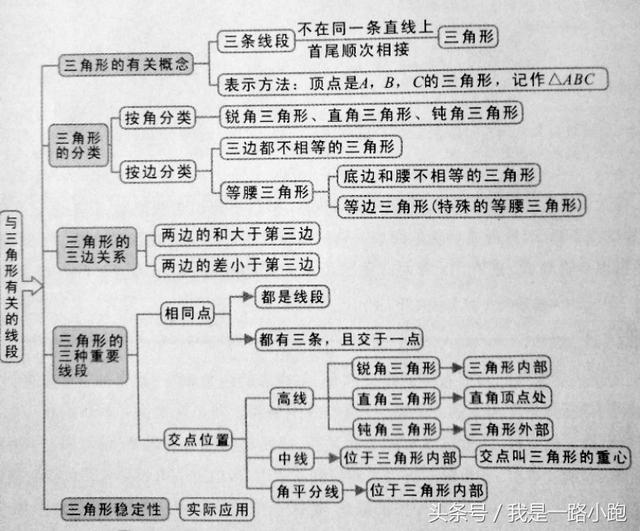
图一: 与三角形有关的线段

下面通过例题分析，来掌握与三角形有关的线段知识的应用

例1: 如图，在△ABC中，D，E分别是BC，AC上的点，连接BE，AD交于F。

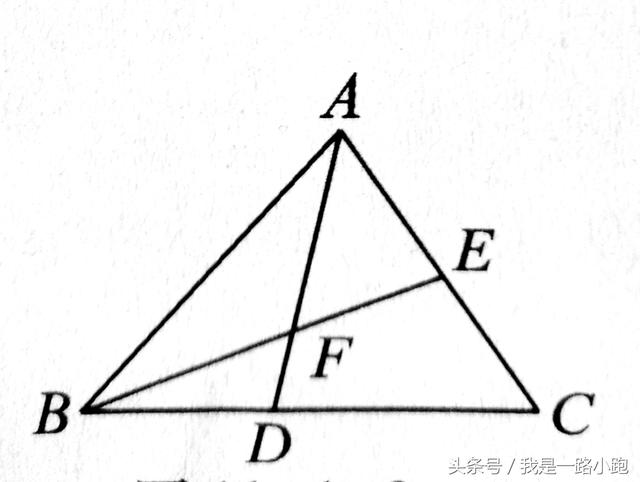
(1) 图中共有多少个三角形?

(2) 以AB为边的三角形有哪些?

(3) 以点F为顶点的三角形有哪些

解: (1) 图中共有8个三角形。

(2) 以AB为边的三角形有△ABF，△ABD，△ABE，△ABC。

(3) 以点F为顶点的三角形有△BDF，△ABF，△AEF。

方法总结:

在复杂图形中数三角形个数的方法:

(一) 按图形形成的过程去数；

(二) 按组成三角形的图形个数去数;

(三) 可从图中的某一条线段开始沿着一定方向去数；

(四) 先固定一个顶点，不断变换另两个顶点来数。

例2 已知等腰三角形的周长等于20cm，一边长等于4cm，求其他两边的长。

解: 分两种情况讨论:

当4cm长的边是底边时，设腰为x cm，则4+x+x=20，解得x=8。

当4cm长的边是腰时，另一腰也是4cm，则底边长为20一4一4=12(cm)

而4+4<12，说明长为4cm，4cm，12cm的三条线段不能组成三角形，所以此种情况不存在。

故三角形其他两边的长均为8cm。

此题是属于用三角形的三边关系解决与等腰三角形有关的问题。对于与等腰三角形有关的问题，一看到就要想是否要分类讨论，另外，必须考虑三条线段能否组成三角形。

例3:如图，已知等边三角形ABc中，AG⊥BC于点G，PD⊥BC于点D，PE⊥AC于点E，PF⊥AB于点F。求证:PD+PE+PF=AG

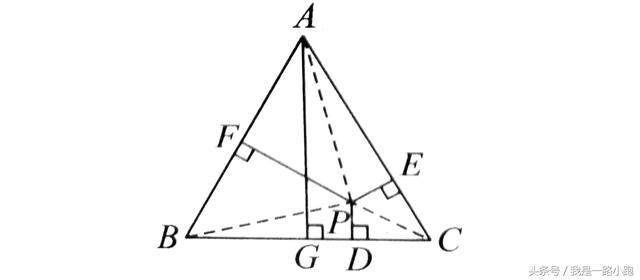
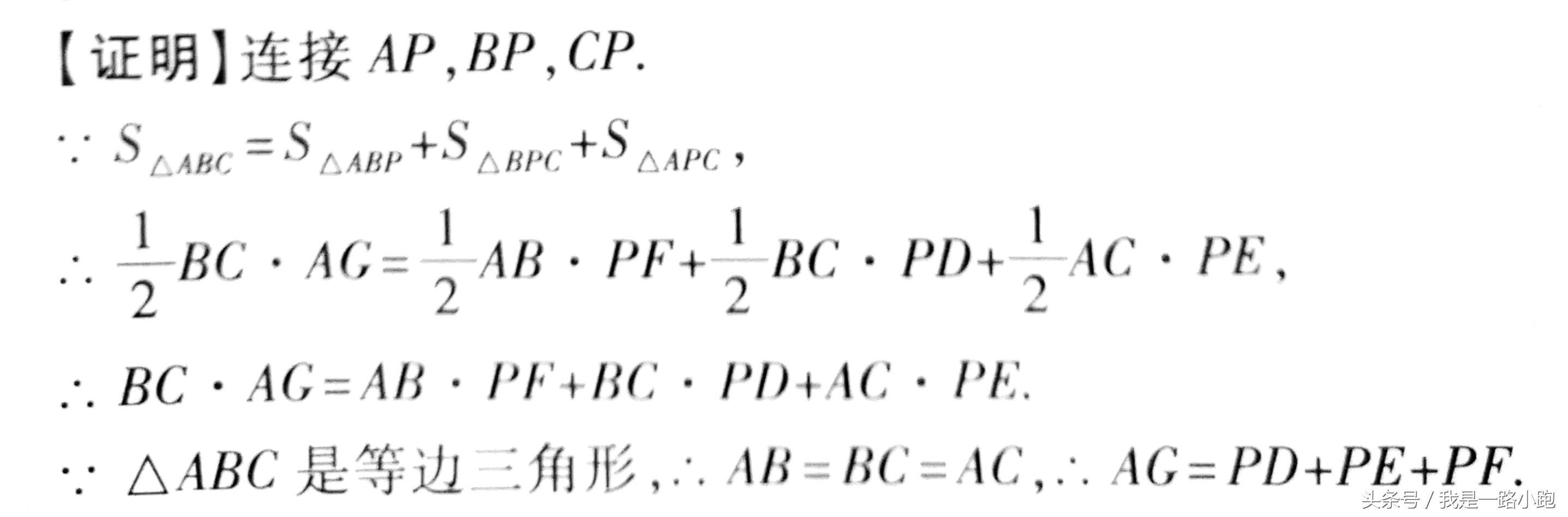
本题运用了等面积法进行解题，根据作辅助线之后的三个小三角形与原三角形面积等列等式。

图二:与三角形有关的角

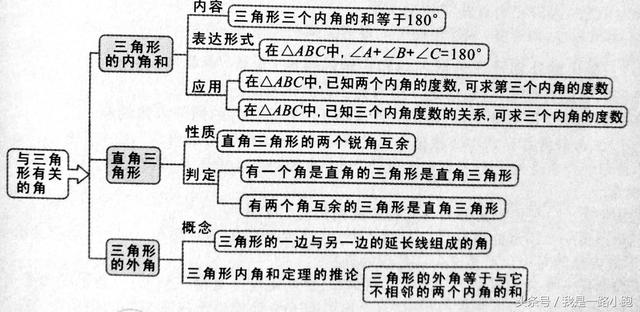
知识应用:

1 直角三角形的判定与性质的运用

2 利用三角形内角和定理及推论解决实际问题

三角形的知识点，要求同学们在弄懂基础知识点的同时，要转化思想，把不可解的问题转化到已学知识范围内可解决的问题。通过转化把不熟悉、不规范、复杂的问题转化为熟悉、规范、简单的问题，再同我们所学的知识解决问题。