八年级16道题：二次根式和勾股定理，基础知识巩固

二次根式，在实数范围内有意义，被开方数大于等于零，若分母有字母的，需要考虑分母不等于零的情况。

4题，无理数的估值，先确定根号20的取值范围，大于4，小于5。所以，1＜m＜2.

7题，这题有很多的理解方法，有一个最简单的理解方法是，n要最大，则根号12-n就会最小。又因为它是正整数，则最小的正整数是1。所以，n的最大值是11.

8题，要注意0次幂的底数，不等于0.

9题，等式变形要去掉绝对值，去掉绝对值要先判定里面的数的正负性，所以根据二次根式的定义，可以得出a-10≥0，所以a-8＞0。绝对值符号成功去掉。

再把二次根式项放左边，其它项移到右边，再等式两边同时平方，即可。

11题，勾股定理最短路径问题，小虫要去吃到内壁的食物G。

这道题，有点类似于将军饮马的问题，作小虫关于杯口的对称点A´，再连接A´G，那么A´G的距离就是最短距离。

12题，这个最短路径问题，就是一个侧面展开图的问题，轻松展开，勾股定理，答案秒出。

13题，这题和11题，题型类似，一样做对称点，再连接即可。

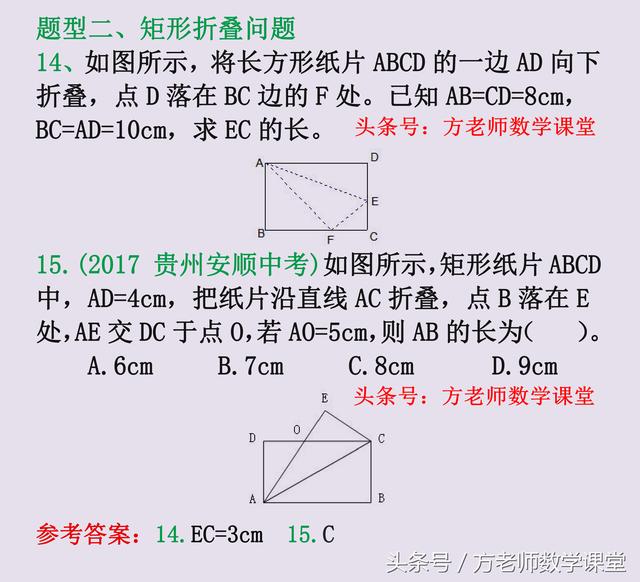
矩形折叠问题，考试常考，经典考试题型。14题，15题，求线段的长度。

这类问题，一般有一个通用的方法，就是设未知数，然后借助图形里的直角三角形，通过勾股定理，构造方程，解方程即可。

题型三、勾股定理距离最短问题的应用，方案选择，经典考试题型。

第1小题，AC=160，BC=120，AB=200，由勾股定理的逆定理，AC²+BC²=AB²得，△ABC是直角三角形。

第2小题，由面积法，算出CH=96米。

甲方案：AC+BC=160+120=280米。乙方案：CH+AH+BH=CH+AB=96+200=296米。280米＜296米，所以，甲方案所修的水渠较短。