初中数学，2018中考数学压轴题热点题型

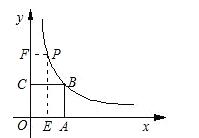
1. 如图，已知：正方形OABC的面积为9，点O为坐标原点，点A在x轴上，点C在y轴上，点B在函数y=k/x(k＞0,x＞0)的图象上，点P(m,n)是函数y=k/x(k＞0,x＞0)的图象上的任意一点，过点P分别作x轴、y轴的垂线，垂足分别为E、F并设矩OEPF和正方形OABC不重合部分的面积为S。

（1）求B点坐标和k的值；

（2）当S=9/2时，求点P的坐标；

（3）写出S关于m的函数关系式。

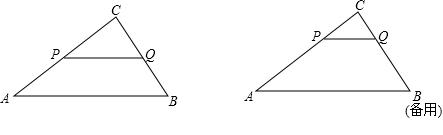
2. 如图：已知△ABC中，AB=5，BC=3，AC=4，PQ∥AB，P点在AC上（与A、C不重合），Q在BC上。

（1）当△PQC的面积与四边形PABQ的面积相等时，求CP的长；

（2）当△PQC的周长与四边形PABQ的周长相等时，求CP的长；

（3）试问：在AB上是否存在一点M，使得△PQM为等腰直角三角形？若不存在，请简要说明理由；若存在，请求出PQ的长。

3. 如图：已知△ABC中，AB＝4，D在AB边上移动（不与A、B重合），DE∥BC交AC与E，连结CD．设S△ABC＝S，S△DEC＝S1．

　　（1）当D为AB中点时，求S1∶S的值；

（2）若AD＝x，S1/S=y，求y关于x的函数关系式及自变量x的取值范围；

（3）是否存在点D，使得S1＞1/4S成立？若存在，求出D点位置；若不存在，请说明理由．