在开始本节内容之前,咱们先把上一节留下的习题解答一下。
看下列叙述正确的是哪个()
1,正数和分数统称有理数。
2,0是整数,但不是正数。
3,-3/8是负分数,2.6不是正分数。
4,既不是正数又不是负数的数一定不是有理数。
正确答案为:B。
有多少人回答正确?为什么是B呢?整数和分数统称有理数,而不单单指正数,所以A错误。0既不是正数,还不是负数,但它是整数,也是有理数,所以B正确,D错误。2.6能化成分数,它是正分数,所以C也错误。
上一节我们知道,正数与负数是相反的。如若我们把有理数表示在一条直线上,规定一方向为正,则另一方向为负,那这条直线有什么特点呢?在画线时要注意什么事项呢?这也就是今天我们要讲的数轴,如下图所示。
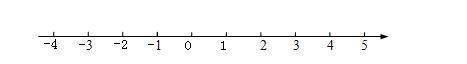
数轴
数轴:规定了原点、正方向和单位长度的直线叫做数轴。
由上我们可以知道,数轴的三要素为:原点,正方向,单位长度。
在画数轴时,三要素缺一不可。数轴一般画成水平的,0点所在的位置就是原点,并以水平向右的方向为正方向,原点位置到下一位置之间的长度为单位长度,通常原点位置和单位长度可任意选取,但一定要适当,同时单位长度应一致。
所有的有理数都可以用数轴上的点来表示,正数可以用原点的右边的点表示,负数可以用原点的左边的点表示,0用原点来表示。这是数与形的初步结合,以后我们还会学到更多的数与形的结合,大家先认真把本节学好,后面才会更得心应手。
观察数轴我们可以知道:
(1)数轴上不同的两个点表示的数,右边点表示的数总比左边点表示的数大,也就是“左小右大”。
(2)1是最小的正整数,没有最大的正整数;-1是最大的负整数,没有最小的负整数。
(3)所有的有理数都可以用数轴上的点来表示,但数轴上的点并不是都表示有理数(也有可能表示以后我们学到的无理数)。
关于数轴的应用,主要是用数轴来比较两个有理数的大小,这个我们可以利用(1)很好的解决,只要画出来数轴,然后把点表示在数轴上,只要是右边点表示的数都比左边点表示的数大。好了,今天也留下一道课后题,请在数轴上把-2,-1.6,-1,0.3,1.2和2表示出来,并判断它们的大小。
好了,今天就到此结束,希望大家认真做一下课后作业,正确的画出数轴,并把数表示出来。

 加载中,请稍侯......
加载中,请稍侯......
精彩评论