数学中关于坐标系任意两点距离计算公式

研究主题：任意两点计算公式

工具：①数轴

②平面直角坐标系

③勾股定理

引申：高中曲线方程中任意圆的解析式。

1.数轴

数轴有三个要素，原点，单位长度和正方向。习惯规定向右(或向上)方向为正方向。

数轴上任意两点间的距离(数学中称之为绝对值)，就是较大数减去较小数[右边的数减去左边的数(如果正方向向上，就是上面的数减去下面的数)]。

如果不知道谁大谁小，或者知道大小，但是不想去思考，那么就的引进绝对值了，既Ιa-bΙ或者√[(a-b)²]

2.平面直角坐标系

理解了数轴，直角坐标系就容易理解了，就是把两根数轴结合在一起，一根竖直方向的数轴，我们称之为Y 轴。一根水平方向的数轴，我们称之为X 轴。

数轴之中任意两点的距离如何计算呢？

别慌，我们还要引进一个新知识点，没错就是勾股定理。

3.勾股定理

简单说下，在一个直角三角形中，两条直角边长度为a和b，斜边长度为c，那么a²+b²=c²

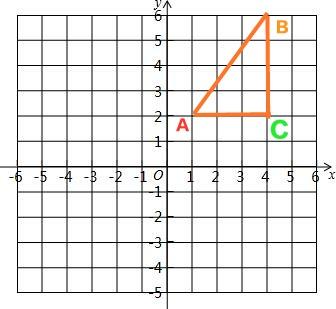
知道了这一点，我们可以计算了。

先假定两点坐标已知，(1,2),(4,6)

则ΙACΙ=√[(1-4)²]=3

ΙBCΙ=√[(2-6)²]=4

ΙABΙ=√[3²+4²]=5

由上可知，如果换成任意未知数(Xa,Ya),(Xb,Yb)，那么两点距离可以这样计算，√[(Xa-Xb)²+(Ya-Yb)²]

实际上，√[(Xa-Xb)²+(Ya-Yb)²]就是中学计算任意两点距离的计算公式。

引申一下，高中阶段会引进圆的方程，而圆的定义初中是这样定义的，到定点(圆心)距离等于定长(半径)的点的集合。所以这个公式是很重要的，理解了这个公式和圆的定义，自己就可以推导出圆的方程。