因式分解进阶——添项、拆项法往往能出奇制胜

因式分解的四个基本方法：

因式分解初步——一定要掌握的四个基本方法

前面还讲一第一种进阶方法，换元法，有兴趣的同学可以去翻看一下。

因式分解进阶——换元法的妙用

今天我们就来研究一下第二种因式分解进阶方法——添项、拆项法。

添项、拆项法原理：

• 因式分解是多项式乘法的逆运算。

• 在多项式乘法运算时，经过整理、化简通常将几个同类项合并为一项，或将两个“只有符号相反的同类项”相互抵消为零。

• 在对某些多项式分解因式时，需要恢复那些被合并或相互抵消的项。

• 即把多项式中的某一项拆成两项或多项（拆项），或者在多项式中添上两个仅符合相反的项（添项）

这几句话虽很长，但它是添项、拆项法的理论基础，多读几十遍，能帮助我们更好地理解、运用添项、拆项法进行因式分解。

好像一不小心铺垫得太长，下面终于要进入正题了！

例1：

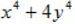
这是一个四次二项式，一般来讲，不好分解的偶次式都可以尝试一下添项变成完全平方，所以首先还是要对公式非常熟悉才行。

有没有发现，这其实就是一个配方法，因为配方法是添项、拆项法的一种特殊情况。当然这个题还可以用待定系数法，会的同学可以自己去试试，待定系数法我们后面会讲到。

看懂的同学能不能用同样的方法做一做下面的题？

例2：

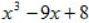
根据一提二套三分组四十字来思考，前两项可以提出一个公因式x，然后用平方差公式，但是接下来没法继续；直接套公式不行；分组分解已经试过了，不行；十字相乘法，不行！上一篇讲的换元法，也不行！

这就是思路，为什么讲数学题还能写这么多字变成一篇一篇的文章呢，是因为我们可以把清晰的思路展现出来。

方法1：

方法2：

方法3：除了拆项，这题也可以考虑一下添项，如果对十字相乘法比较熟悉，就会发现原式后两项比较接近十字相乘法，我们来试试,

想想还有别的方法吗？

通过这个题我们可以发现，需要添加的项和需要拆开的项都是不固定的，思路灵活多变，所以我们做题时一定要认真观察，仔细思考，多做尝试，千万不要怕错，错多了有了经验，慢慢的正确率就会越来越高。

添项、拆项法，是因式分解众多方法中较为灵活的一种，它不像四种基本方法一样简单，也没有待定系数法那些难解的方程组，但它是技巧性最强的、最能锻炼我们思维能力的因式分解方法。

十字相乘法虽然在书本上没有做要求，但是我们经常在遇到十字相乘法的题目，而且有时候解二元一次方程也能够用到，十字相乘法是待定系数法的特殊形式，在后面会专门讲到。

总的来说，我们在做因式分解时，首先考虑四个基本方法，然后再尝试各种进阶方法，往往需要各种方法反复多次使用，才能得出最终结果，所以，希望大家能够掌握我提到的每一种方法。