人教版七年级上册——一元一次方程的解法

一 知识归类

1. 方程的有关摡念

(1) 方程

含有未知数的等式叫做方程。如3x+6=12，判断一个式子是不是方程，必需看两点；①是等式，②是含有未知数，两者缺一不可。

(2) 方程的解

使方程中等在右两边相等的未知数的值，叫做方程的解，只含有一个未知数的方程的解，也叫做方程的根。

(3) 解方程

求方程解的过程，叫做解方程。

2 一元一次方程

(1)概念:只含有一个未知数(元)，未知数的次数都是1，等号两边都是整式，这样的方程叫做一元一次方程。

(2)判别方法

判断方程是否为一元一次方程，需同时满足:①只含有一个未知数；②末知数的次数都是1；③是整式方程。三个条件，缺一不可。

3等式的性质

(1)性质1

等式两边加(或减)同一个数(或式子)，结果仍相等

如果 a=b，那么a+c=b+c；a-c=b-c。

(2)性质2

等式两边乘同一个数，或除以同一个不为0的数，结果仍相等。

如果 a=b，那么 ac=bc；如果a=b(c≠0)，那么a/c=b/c

3 解一元一次方程方法及步骤

(1) 合并同类项

与整式加减中所学的内容相同，将等号同侧的含有未知数的项和常项分别合并成一项的过程叫做合并同类项。合并同类项的目的是向接近x=a的形式变形，进一步求出一元一次方程的解。

(2) 移项

①概念:把等式一边的某项变号后移到另一边，叫做移项。

②依据:移项的依据是等式的性质1。

③目的:通常把含有未知数的各项都移到等号的左边，而把不含未知数的各项都移到等号的右边，使方程更接近于x=a的形式。

(3)系数化为1

①概念:将形如ax=b(a≠0)的方程化成x=b/a的形式，也就是求出方程的解x=b/a的过程，叫做系数化为1。

②依据:运用等式的性质2，方程左右两边同时乘未知数系数的倒数。

(4)去括号

解方程过程中，把方程中含有的括号去掉的过程叫去括号。

(5) 去分母

①去分母方法:一元一次方程的各项都乘所有分母的最小公倍数，依据等式的性质2使方程中的分母变为1。

②去分母的依据:是等式的性质2，即在方程的两边都乘所有分母的最小公倍数，使方程的系数化为整数。

我们在解一元一次方程的基本思想是把原方程化为ax=b(a≠0)的形式，其解法可分为两大步:①是化为ax=b(a≠0)的形式，②是解方程ax=b

一般来说，解方程就是以上5个步骤，但在解具体的方程时有些可能用不到，可根据方程的特点灵活选用。

二 例题讲解

例 求下列方程的解。

2x-(9x-3)=10

解 去括号得 2x-9x+3=10

移项得 2x-9x=10-3

合并类项得 -7x=7

系数化为1得 x=-1

[点评]本题主要考查去括号、合并同类项、移项的基本方法。

[点评]分数的基本性质与等式的基本性质不要混淆。

三 真题练习

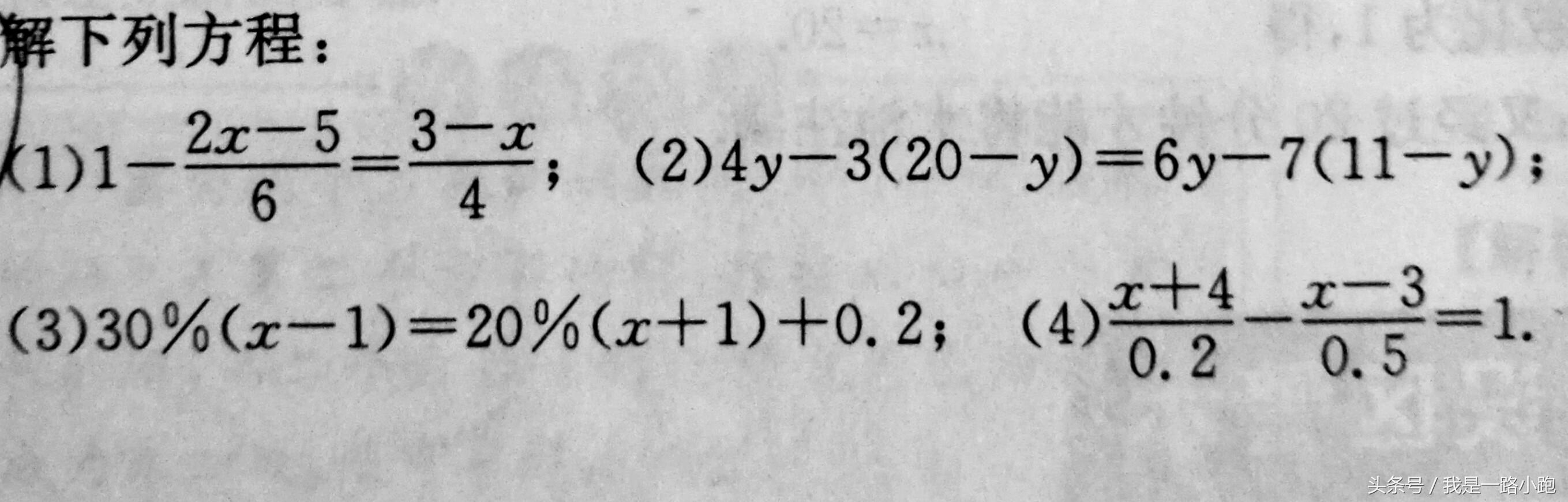
习题练习，加强知识记忆，轻松学好一元一次方程。