因式分解进阶——换元法的妙用

换元法

换元法又称变量替换法，即对结构比较复杂的多项式，若把其中某些部分看成一个整体，用新字母代替(即换元)，则能使复杂的问题简单化，明朗化，在减少多项式项数,降低多项式结构复杂程度等方面有独到作用。

-----引自百度百科

上面的文字看起来有点懵，我们通俗一点讲就是，把某个式子看成一个整体用一个变量（字母）去替代它，从而使问题简化，这就叫换元法。

换元法是整体思想的体现，是非常重要的数学思维，也是高中阶段常用的数学方法，希望大家能好好研究一下。

数学解题思想之整体思想，快看看你家孩子会不会

一、整体换元

例1：

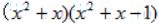
乍一看，好像能提公因式，但是当我们尝试后发现，提完公因式就没法继续下一步了，后面的括号里也不满足十字相乘法，所以，我们今天使用换元法。

整体换元法通常把相同的部分设为一个字母。

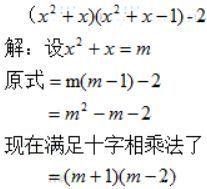
整体换元

我们可以看到，在综合练习中，一般不会只使用一种方法就解分解完全，一定是几个方法来回不断地使用，所以我们一定要记住每一种方法，并养成检查的习惯。

二、均值换元

顾名思义，均值换元法就是求出两个部分的平均值，然后把这个平均值设为字母。

例2：

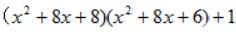
仔细观察，两个括号中式子相差2，很容易求出他们的平均值：

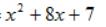
所以，我们可以这样做：

均值换元

三、双换元

有时候根据题目需要，我们可以用双换元法，把其中的两个部分，分别设为两个字母，然后再根据和差关系推导出另外的部分，再代入原式进行分解。

例3：

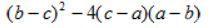
很明显，c-a、a-b、b-c这三个式子是首尾相连的，很容易得到他们的关系。

双换元

还有两种比较罕见的换元法，正常的考试中碰到这类题的机率很小了，但是可以做一个了解，增加一下自己的认知度。

四、倒数换元

例4：

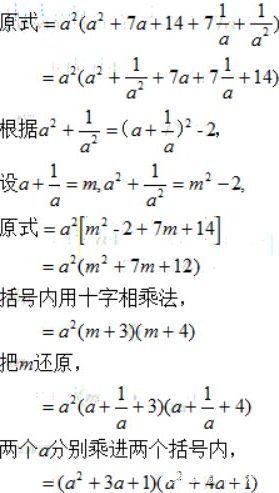
倒数换元

这个题目没有太多需要讲的，基本上是比较佛系的题了，随缘，能碰到对的思路就对了，碰不到，可能想破脑袋都难想出思路。但是提公因式后的设元，还是值得研究推敲！

五、和差换元

和差换元可以算是均值换元的进阶版，脑路清奇的可以记住有这么个方法，一般情况下用不到，我们直接来看个例题吧。

例5：

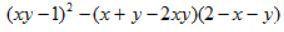
面对这种三项式乘以三项式的，一般都要考虑换元法，我们先用灵光一闪的和差换元做一下：

和差换元

不过，这个题我们也可以直接采用双换元法，思路要清晰一点，算是有迹可寻。我们再把题目看一次，找一下思路。

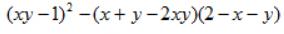
还是上面的例题哈

通过对题目的观察，发现里面x+y和xy是重复出现的，那就直接设它们好了。

例5的第二种解法