中考数学分类讨论思想在解决相似图形问题中的应用

图形的相似这一节是平面几何中极为重要的内容，也是中考数学中的重点考查内容。三角形相似常常与三角形全等、四边形、函数等联系，利用动点变化，探究图形的特殊形状、点的坐标或变量之间的函数关系。

解决此类问题的关键是要掌握相似的基础知识，在理解题意的基础上运用相似的知识会解决一些实际问题；而在综合题中，会灵活运用相似的知识，熟练掌握等线段代换、等比代换、等量代换技巧的应用，培养综合运用知识的能力。

本文主要来介绍下分类讨论思想在解决相似图形问题中的应用，对于中考数学压轴题中出现此类相似图形的问题是大有帮助的！

一、判定三角形相似的几条思路

1、条件中若有平行线，可采用相似三角形的基本定理；

2、条件中若有一对等角，可再找一对等角或找夹边成比例；

3、条件中若有两边对应成比例，可找夹角相等；

4、条件中若有一对直角，可考虑在找一对等角或证明斜边、直角边对应成比例；

5、条件中若有等腰关系，可找顶角相等，可找一对底角相等，也可找底和腰对应成比例。

二、相似基本图形

1、“A”字型

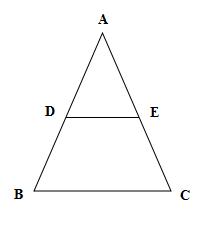
A字型

若 DE∥BC ，则 △ADE∽△ABC ；

2、“8”字型

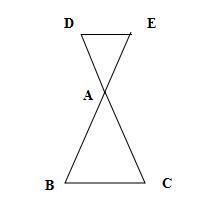
8字型

若 DE∥BC ，则 △EAD∽△BAC ；

3、“A'”字型

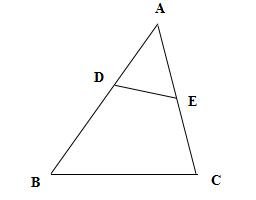
A'字型

若 ∠AED = ∠B ，则 △AED∽△ABC 。

三、相似三角形的性质

1、相似三角形的对应边的比等于相似比；

2、相似三角形的周长比等于相似比，面积比等于相似比的平方；

3、相似三角形对应边上的高、中线、角平分线的比都等于相似比。

四、应用分类讨论数学思想解决相似图形问题

对于题目中给出的条件，不能确定其结论的唯一性时，需要对可能存在的情况进行分类讨论。尤其在说明两个三角形相似时，应将对应字母写在对应位置上，如果题目中没有说明，即只是说两个三角形相似，则需要分类讨论。

例题1、已知在 △ABC 中，AB = 8 , BC = 7 , AC = 6 , 点 D、E 分别是 AB、AC 边上的动点（不与点 A、B、C 重合），如果以 A、D、E 为顶点的三角形和以 A、B、C 为顶点的三角形相似，且相似比为 1 ： 4 ，试求线段 AD 和 AE 的长 。

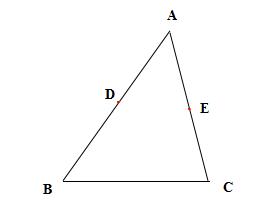
解题思路：此题属于典型的分类讨论题型，在动点的运动过程中，会形成两种最基本的相似图形“A”字型和“A'''字型，解题过程如下：

解：

① “A”字型，如图所示：

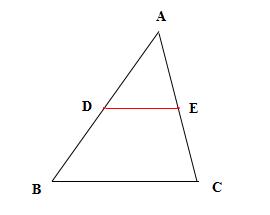
当 △ADE∽△ABC 时，由相似三角形的性质可得：

AD : AB = AE : AC = 1 : 4 ,

即 AD ： 8 = AE ：6 = 1 ： 4 ，

所以 AD = 2 , AE = 1.5 ；

② “A'”字型，如图所示：

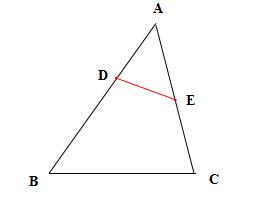
当 △AED∽△ABC 时，由相似三角形的性质可得：

AE : AB = AD : AC = 1 : 4 ,

即 AE ： 8 = AD ：6 = 1 ： 4 ，

所以 AD = 1.5 , AE = 2 ；

综上：AD 等于 2 或 1.5 ，AE 等于 1.5 或 2 。

评注：题目中所给出的条件仅表明两个三角形具有相似关系，并没有明确指出它们的对应点，因此在动点的运动过程中需要分类讨论，列举出可能出现的情形。

例题2、如图，在梯形 ABCD 中，AD∥BC ，∠A = 90°，AB = 7 ，AD = 2 ，BC = 3 。试问在线段 AB 上是否存在一点 P ，使得以 P、A、D 为顶点的三角形和以 P、B、C 为顶点的三角形相似？若不存在请说明理由；若存在，这样的 P 点共有几个？并求出线段 AP 的长 。

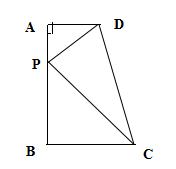
解：假设满足条件的点 P 存在，则有以下两种情形：

① 当 △APD∽△BPC 时，由相似三角形的性质有：

AP : BP = AD : BC , 即 AP : BP = 2 : 3 ,

因为 AP + BP = AB = 7 ,

所以 AP = 14/5 .

② 当 △APD∽△BCP 时，由相似三角形的性质有：

AP : BC = AD : BP , 即 AP : 3 = 2 : ( 7 - AP ) ,

所以 AP = 1 或 6 。

综上：存在这样的点 P ，使得以 P、A、D 为顶点的三角形和以 P、B、C 为顶点的三角形相似，且这样的点 P 共有 3 个，线段 AP 的长分别为 14/5 或 1 或 6 。

分类讨论题目是中考数学中常见的考题，对于题目中给出的条件，不能确定其结论的唯一性时，需对可能存在的情况要注意进行分类讨论！