1、三角形的面积平分
①三角形的中线将三角形面积平分
②构造以下模型,通过等面积转换,作出面积平分线
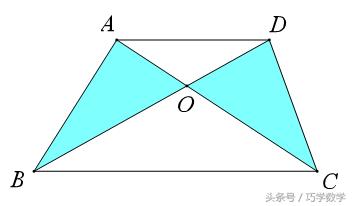
如图,在梯形ABCD中,易证△OAB和△OCD面积相等,我们不妨称之为“蝴蝶模型”。
构造蝴蝶模型的关键点:平行线
构造蝴蝶模型的目的:等面积转换
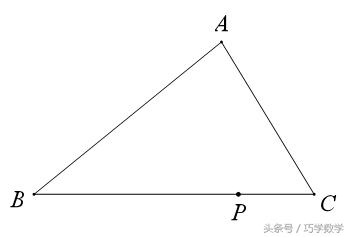
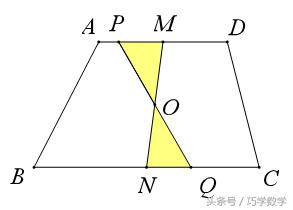
例1、如图,过△ABC的底边BC上一定点P,求作一直线l,使其平分△ABC的面积.
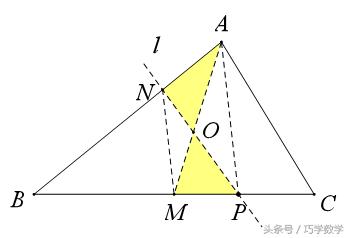
简答:取BC中点M,连接AM,则△ABM和△ACM的面积相等,连接AP,过M作AP的平行线MN,构造“蝴蝶模型”如图,∵△OAN和△OPM面积相等,∴△BNP和四边形ACPN面积相等。
2、平行四边形的面积平分
结论1:过平行四边形中心的任意一条直线,平分该平行四边形的面积。
结论2:任何图形,只要能找到它的中心,那么过中心的直线平分这个图形的面积。
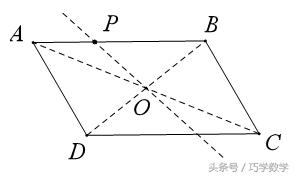
例2、如图平行四边形ABCD中,点P是AB边上一点,过点P求作一条直线,使其平分平行四边形ABCD的面积。
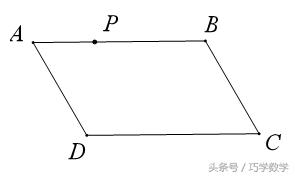
简答:连接BD、AC交于O点,则直线PO即为所求作的直线。可用全等证明,过程略。
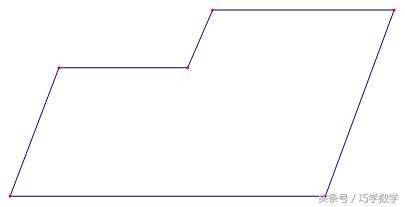
例3、现有如图的铁片,其形状是一个大的平行四边形在一角剪去一个小的平行四边形,工人师傅想用一条直线将其分割成面积相等的两部分,请你帮师傅设计三种不同的分割方案.
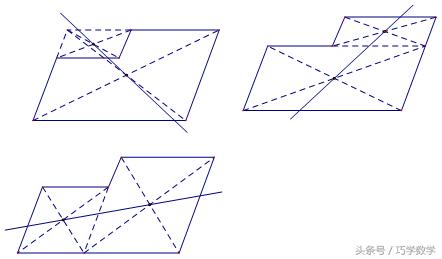
简答:如图所示,三种方法都是取大小两个平行四边形的中心,连接即可。
3、梯形的面积平分
结论1:梯形上下底中点的连线平分该梯形的面积。
结论2:过梯形上下底中点的连线的中点,且与上下底有交点的直线,平分该梯形的面积。
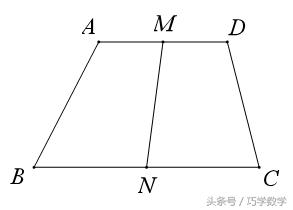
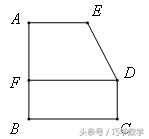
例4、如图:五边形ABCDE可以看成是由一个直角梯形和一个矩形构成.
⑴ 请你作一条直线,使直线平分五边形ABCDE的面积;
⑵ 这样的直线有多少条?请你用语言描述出这样的直线.
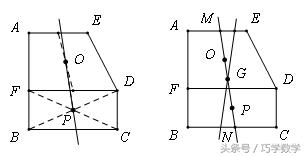
简答:(1)取梯形上下两底中点连线的中点O,取矩形的中心P,则直线OP即为所求作直线l;
(2)这样的直线有无数条,设直线l与AE交于M,与BC交于N,取MN中点G,则过G点且与线段AE、BC均有交点的直线平分五边形ABCDE的面积。
4、不规则四边形的面积平分
对于不规则图形,如何作面积平分线呢?
如图四边形ABCD,过A点求作一条直线,使其平分四边形的面积。
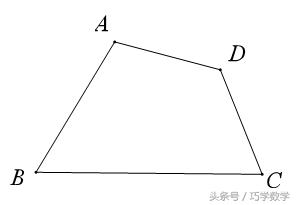
做法:连接AC,过D作AC的平行线与BC延长线交于M点,连接AM,取BM的中点G,则直线AG平分四边形ABCD的面积。
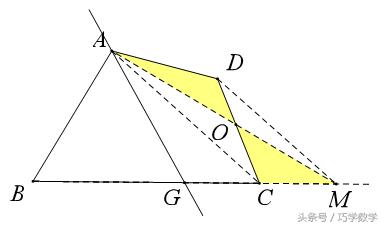
理由如下:由“蝴蝶模型”知△AOD和△COM的面积相等,则△AGM和四边形AGCD的面积相等,又∵△AGM和△AGB的面积相等,∴△AGB和四边形AGCD的面积相等。
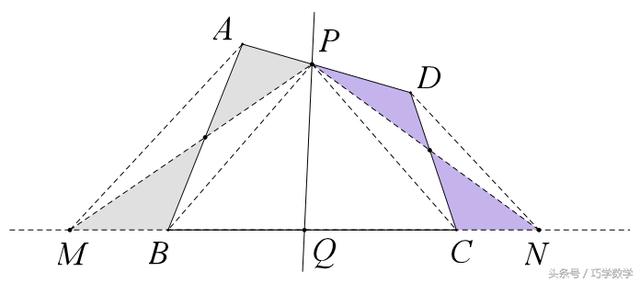
例5、过四边形ABCD的边AD上一点P,作一条直线,使其平分四边形的面积。
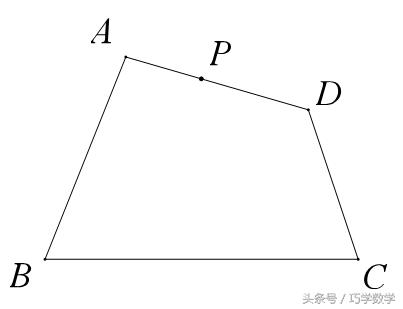
做法:连接PB、PC,过A作PB的平行线,过D作PC的平行线,与BC延长线分别交于M、N两点,连接PM、PN,取MN的中点Q,则直线PQ平分四边形ABCD的面积。
证明略
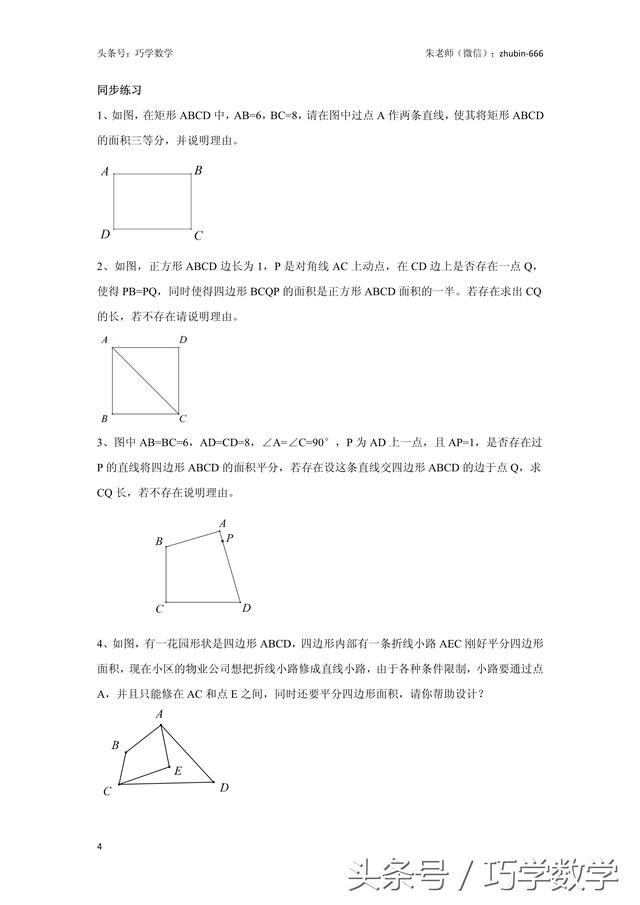
同步练习:

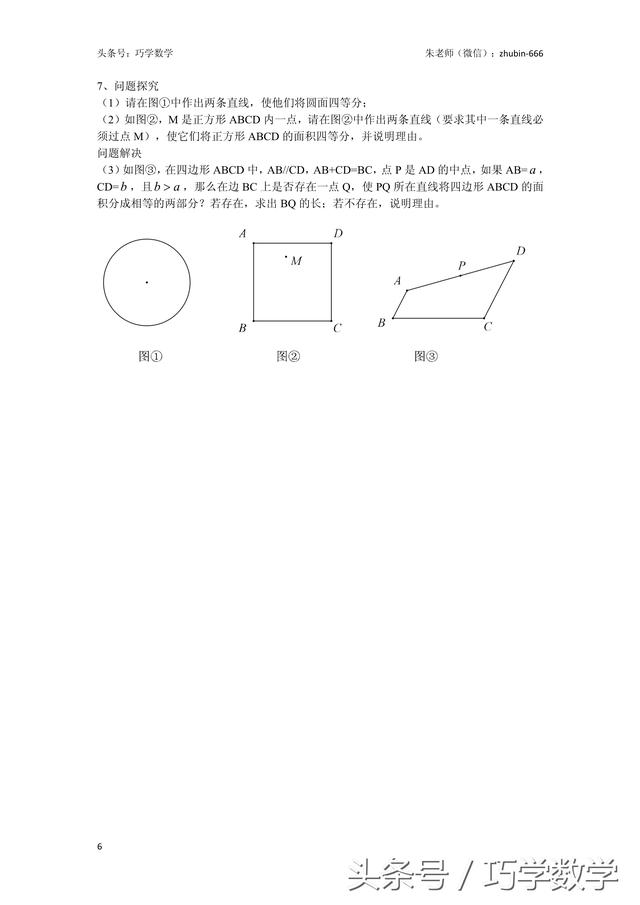

 加载中,请稍侯......
加载中,请稍侯......
精彩评论