五种全等三角形辅助线作法，见招拆招，解决几何难题的好帮手

第一种，我们称呼为倍长中线造全等。什么意思呢，就是当题目的已知条件里面出现中线这个几何特征的时候，在我们在初始图像中找不到很好的解题突破口的情况下，我们可以考虑延长这条中线（一般是延长一倍形成相等边）来构造全等三角形，从而揪出更多的可用条件，为解题另辟蹊径。

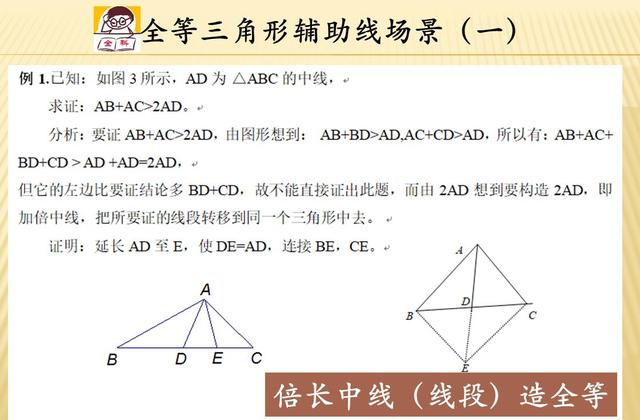
第二种，我们称呼为截长补短法。顾名思义就是在某一条线段或者边上截取一段或者延长一段，使它构成特殊的特征（一般是相等），这样可以构造出全等三角形的一些边角关系，特别适用于证明线段的和、差、倍、分等类的题目。比如下题中的求证BE+CF>2AD的边长和关系。

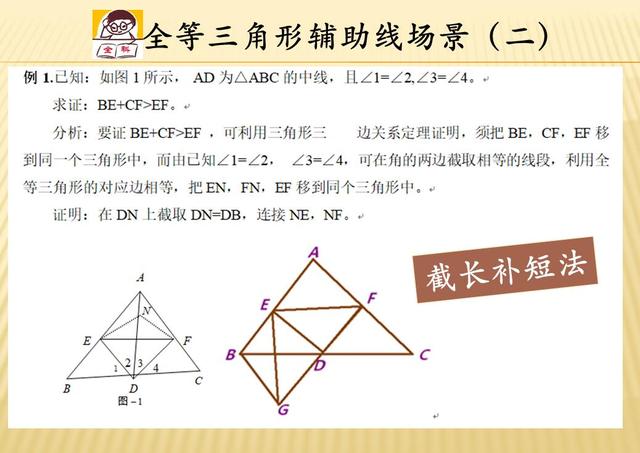
第三种是利用等腰三角形三线合一的性质进行构造全等三角形。我们知道等边三角形底边上的高线也是中线和角平分线（三线合一），所以当题目出现等腰三角形或者你能够通过简单的几何关系找出等腰三角形之后，你可以尝试做出这根特殊的线条来帮助你思考，比如下题中的取AB中点E，连接DE即可得出这根特殊的线段和全等三角形的一些判定和性质应用。

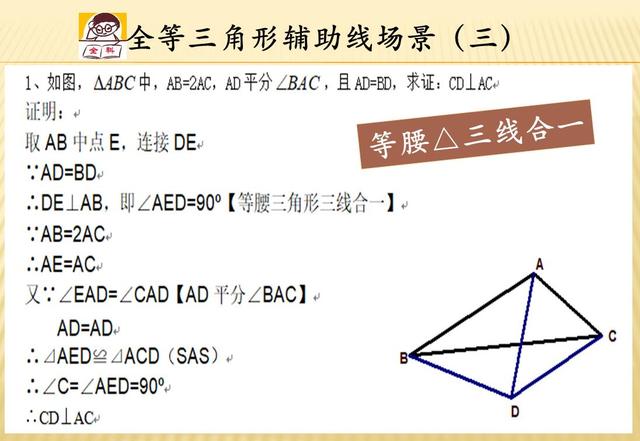
第四种，利用角平分线的性质，我们知道过角平分线上任一点作两边的垂线，得出的这两条线段长度相等，如果我们这样构造，相当于又得到了一些特殊的边角关系来作为我们思考的小组手。

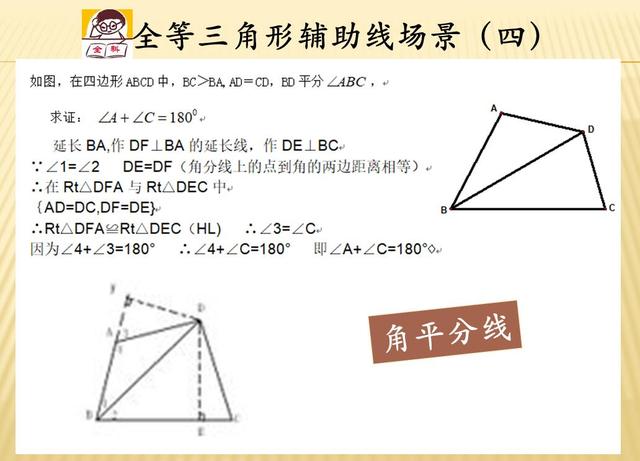
第五种，利用角平分线性质构造全等变换中的“平移”或“翻转折叠”，这样也能轻松形成一些全等的三角形，从而得出解决问题的一些关键隐藏条件。这是比较难想到的一种辅助线思路，具体可以通过下面这道题来细细体会。

写在最后：以上五种全等三角形辅助线作法，只是基础的构图法，并非一定要这样或者非如此不可，这需要大家在练习的过程中融会贯通，方法是死的，只有思路才是活的，学会之后要灵活应变，就像太极中的无招胜有招，才能见招拆招！犹记得张三丰太师傅问无忌：你记住这些招式了吗？忘了最好！