八年级数学一次函数的图像及性质（1）

一、函数的图像

把一个函数的自变量 x 与对应的因变量 y 的值分别作为点的横坐标和纵坐标 , 在直角坐标系内描出它的对应点 , 所有这些点组成的图形叫做该函数的图象。

例：

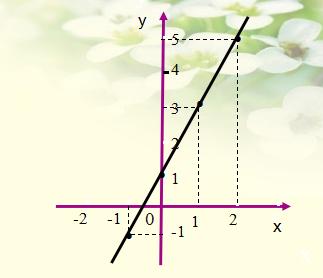
一次函数 y=2x+1 的图像

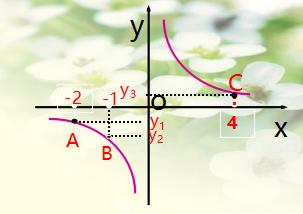
反比例函数 y=k/x(k>0) 的图像

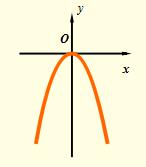
二次函数 y=ax^2(a<0) 的图像

二、函数的图像及画法

1、画函数图像的一般步骤：(1)列表；(2)描点；(3)连线 。

2、函数图像与点的坐标的关系：

① 函数图像上的任意点 P(x，y) 必满足该函数表达式 ；

② 满足函数表达式的任意一对 x，y 的值，所对应的点一定在该函数的图像上 ；

③ 判断点 P(x，y) 是否在函数图像上的方法：

将点 P(x，y) 代入函数表达式，如果满足函数表达式，那么这个点就在函数的图像上；如果不满足函数的表达式，那么这个点就不在函数的图像上 。

例题1、已知一次函数 y=kx+2，当x=-1时， y=1，求此函数的表达式，并在平面直角坐标系中画出此函数的图像。

注：本题主要考查利用待定系数法求函数的表达式和利用“两点法”作一次函数图像，根据两点确定一条直线作出图像是解答此题的关键。

三、正比例函数的图像和性质

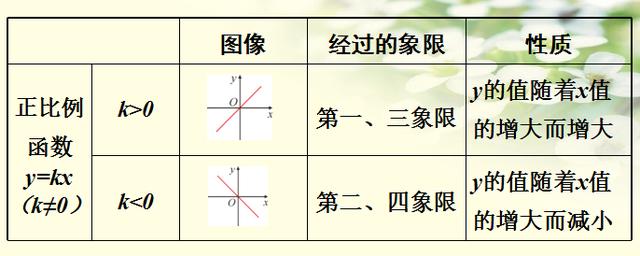
注：正比例函数 y=kx（k≠0）的图像是经过原点（0，0）的一条直线，反之，如果函数图像是直线且经过原点（除坐标轴外），那么它对应的函数就是正比例函数 。

四、一次函数的图像与性质

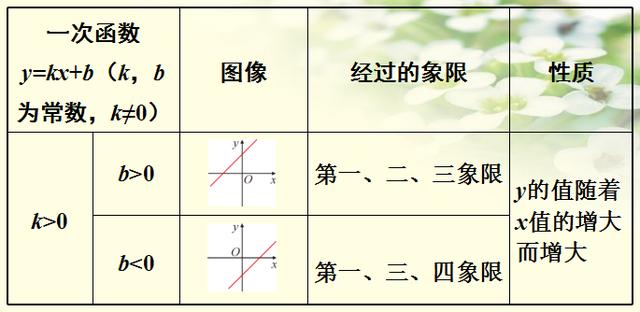
k>0

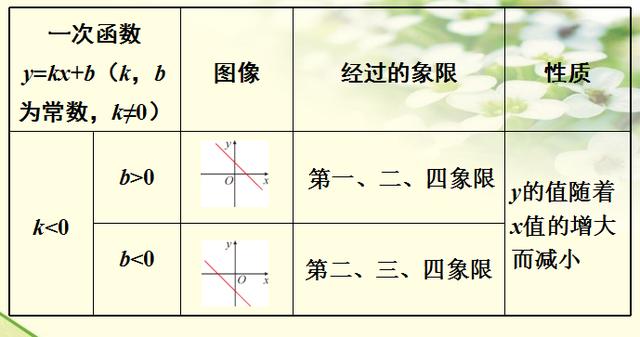
k<0

注：

① k 决定一次函数y=kx+b（k≠0）的增减性，b 决定函数图像与 y 轴的交点位置 ；

② 通过图像可知一次函数 y=kx+b（k≠0）的图像是一条直线。

根据“两点确定一条直线”的性质，画一次函数的图像时只要找出两个点，再过这两个点作直线就可得到一次函数的图像。

一次函数的图像与 y 轴的交点坐标是（0，b），与 x 轴的交点坐标是(-b/k，0)，画图像时通常选取这两个特殊点 。

例题2、关于直线 l：y=kx+k（k≠0），下列说法不正确的是（D ）

A、点（0，k）在 l 上

B、l 经过定点（-1，0）

C、当 k＞0 时，y 随 x 的增大而增大

D、l 经过第一、二、三象限

例题3、已知一次函数 y=mx+n 的图像不经过第二象限，求m，n 的 取值范围。

解：由题意，得一次函数 y=mx+n 的图像经过第一、三、四象限或第一、三象限，

所以 m>0，且 n≤0。

注：要判断一个函数是否为一次函数，就是要通过恒等变形，把它转化为y=kx+b的形式，

即 x 的次数为 1，且 k≠0，b 为任意常数，否则它就不是一次函数，解题过程中易忽略 k≠0这个条件，导致出错。

例题4、若直线 y=kx-4 与两坐标轴所围成的三角形的面积是 4，求该直线的解析式

五、知识拓展与提高

① |k|与直线的倾斜程度：

|k| 的大小决定直线的倾斜程度，|k|越大，直线越陡；|k|越小，直线越缓；

② 正比例函数y=kx（k≠0）的图像与一次函数 y=kx+b（k≠0）的图像的位置关系：

二者的图像都是直线，且互相平行；

平移关系：

直线y=kx（k≠0）向上（b>0）或向下（b<0）平移|b|个单位长度，就能得到直线y=kx+b（k≠0）；

反之将直线y=kx+b（k≠0）向下（b>0）或向上（b<0）平移|b|个单位长度，就能得到直线 y=kx（k≠0）。

例题5、已知正比例函数 y=kx 的图像经过点 A，点 A 在第四象限，过点 A 作 AH⊥x 轴，垂足为 H，点 A 的横坐标为3，且 △AOH 的面积为 3。

(1) 求正比例函数的表达式 ;

(2) 在 x 轴上能否找到一点 P，使 △AOP 的面积为 5？ 若存在，求出点 P 的坐标；若不存在，请说明理由。

解题思路：

（1）先根据题意求出点 A 的坐标，再利用待定系数法求出正比例函数的表达式；

（2）先利用三角形的面积公式求得 OP=5，再根据坐标与图形的性质求得点 P 的坐标。