「初中数学」构造等边巧妙求角

通过构造等边、巧妙求角的问题，本文整理了一些题目，仅供参考一

例1

如图，已知在△ABC中，AB=BC，∠ABC=90°，AB=AE，∠BAE=30，

求证：BE=CE

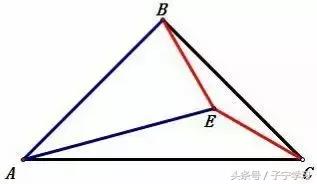
分析

标注图中每个已知或易知角的度数

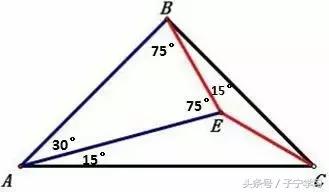
通过"等角对等边"证明"BE=EC"的关键在于证明∠BCE=15°或∠ECA=30°，直接证似不可行，需要添加辅助线，进行边角的转化…

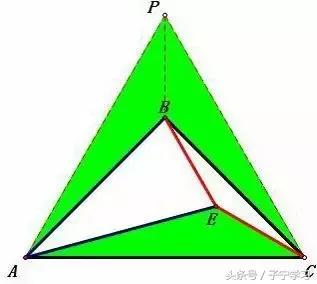
解法一

① 构造等边△APC

（做∠MAC=60°，在AM上截取AP=AC，联结PC）

② 证△APB≌△PBC

（AP=PC，AB=BC，PB=PB）

③ 证△APB≌△AEC

（AB=AE，∠PAB=∠EAC=15°，AP=AC）

④ ∠ECA=∠APB=30°

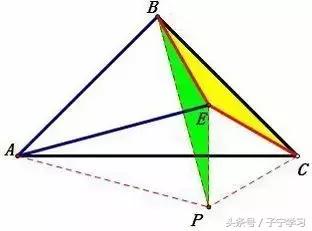
解法二

① 构造等边△APB

（做∠BAM=15°，在AM上截取AP=AB，联结BP、EP）

② 求∠BPE

（在△AEP中，∠EAP=30°，AE=AP，则∠APE=75°，继而可得∠BPE=15°）

③ 证△BEP≌△BEC

（PB=AB=BC，∠PBE=∠EBC=15°，BE=BE）

④ ∠BCE=∠BPE=15°

解法三

① 构造等边△PBE

（做∠EBM=60°，在BM上截取BP=BE，联结EP）

② 证△APB≌△APE

（AP=AP，AB=AE，PB=PE）

③ 证△APB≌△BEC

（AB=BC，∠ABP=∠EBC=15°，BP=BE）

④ ∠BCE=∠BAP=∠EAP=15°

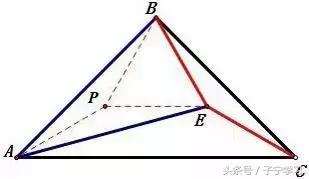
例2

如图，已知在△ABC中，AB=AC，∠A=20°，若AD=BC，求∠BDC

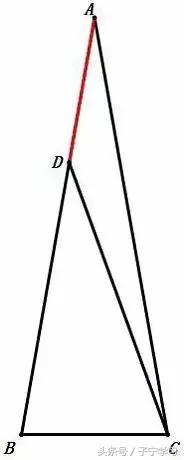
分析

20°角为顶角的等腰三角形是一个很有趣的三角形，其中蕴含了很多经典的几何问题，这是其中较简单的一道。

由于已知∠A=20°，所以求∠BDC重在求∠ACD，另外如何使用“AD=BC”这一条件也很关键…

解法一

① 构造等边△BPC

（做∠MBC=60°，在BM上截取BP=BC，联结PC、AP）

② 证△APB≌△ABC

（BP=PC，AB=AC，PA=PA）

③ 证△APB≌△ADC

（AD=BC=BP，∠ABP=∠DAC=20°，AB=AC）

④ ∠ACD=∠BAP=10°

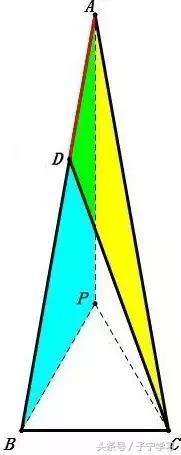
解法二

① 构造等边△ACP

（做∠CAM=60°，在AM上截取AP=AC，联结PC、PB）

② 证△ADP≌△ABC

（AD=BC，AP=AC，∠ACB=∠BAP=20°+60°=80°）

③ 求∠DCP

（在△DCP中，DP=AB=CP，∠DPC=60°-20°=40°，∠DCP=70°）

④ ∠ACD=70°-60°=10°

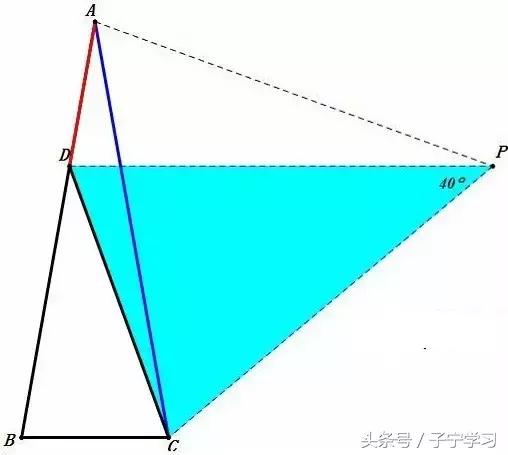
解法三

① 构造等边△ABP

（做∠BAM=60°，在AM上截取AP=AB，联结PB、CP）

② 求∠BPC

（在△ACP中，AP=AB=CA，∠PAC=60°-20°=40°，∠APC=70°，∠BPC=70°-60°=10°）

③ 证△BCP≌△ADC

（AD=BC，∠BAC=∠PBC=20°，AB=AC=BP）

④ ∠ACD=∠BPC=10°

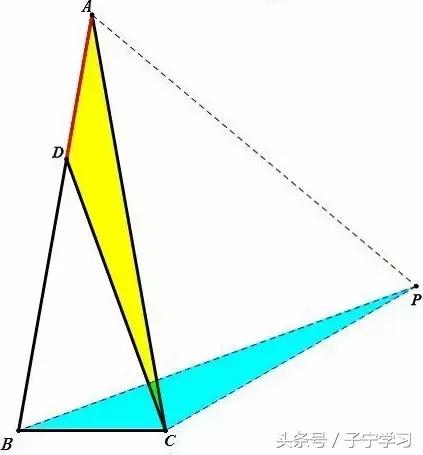
以下两题与本帖两例类似，供大家尝试…

类题1

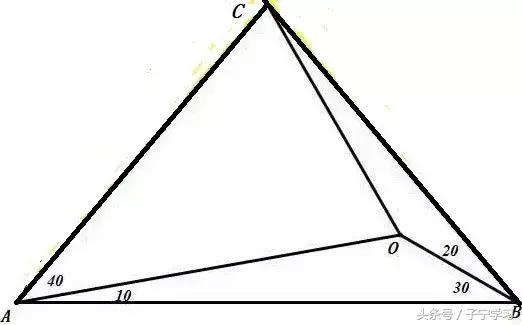
如图，已知在△ABC中，AC=BC，∠ACB=80°，O为△ABC内一点，∠OAB=10°，∠OBA=30°，求∠ACO的度数

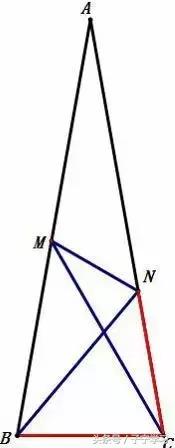
类题2

如图，已知在△ABC中，AB=AC，∠A=20°，∠NBC=50°，∠BCM=60°，求∠NMC