周长最值问题

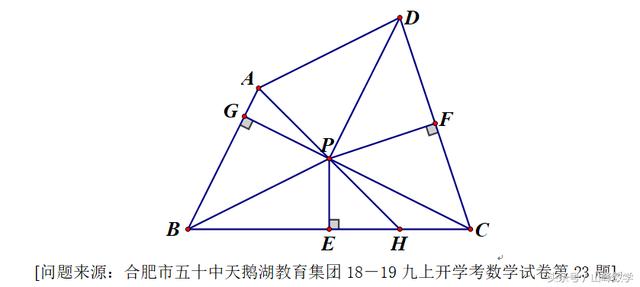
四边形ABCD中，AB＝AD，PE、PF分别是边BC、CD的中垂线，连接PA、PB、PC、PD，延长AP交BC于点H，延长CP交AB于点G，若AD∥BP，CG⊥AB。

(1)判断四边形ABPD的形状，并加以证明；

(2)证明：∠AHB＝45°；

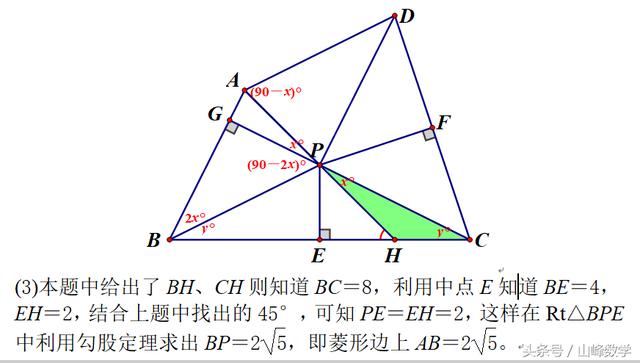
(3)若BH＝6，CH＝2，求AB的长度。

【问题简析】

（1）四边形ABPD中(如下左图)，由已知条件知道(如下右图)红色线段相等AB＝AD；利用垂直平分线的性质知道PB＝PC＝PD；这样四边形中有两组邻边相等，又AD∥BP，因此可猜想该四边形可能为菱形。

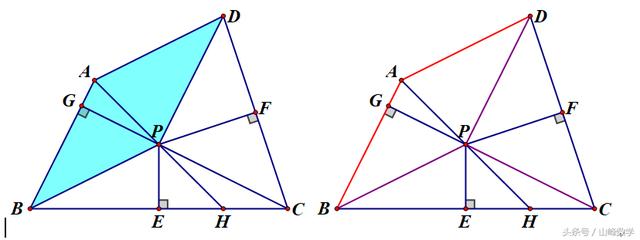
在这个四边形中，易证△APB≌△APD(SSS)，从而知道∠1＝∠2，∠4＝∠3，又因AD∥BP，所以有∠1＝∠3，这样∠1＝∠2＝∠3＝∠4，所以有AB∥PD，两组对边平行所以是平行四边形，再加上有邻边相等，所以所求四边形为菱形。

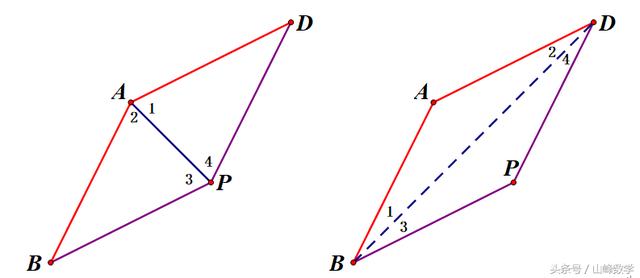
本题也可考虑利用连接BD，可得到如下图形式，利用等腰三角形知道∠1＝∠2，∠3＝∠4，再利用AD∥BP，所以有∠2＝∠3，这样再次产生出∠1＝∠4，获得AB∥PD

(2)本小题要找45°角，考虑到所在三角形已经是直角三角形，但另一个内角也难以找出45°，因此可考虑运用外角协助找到。

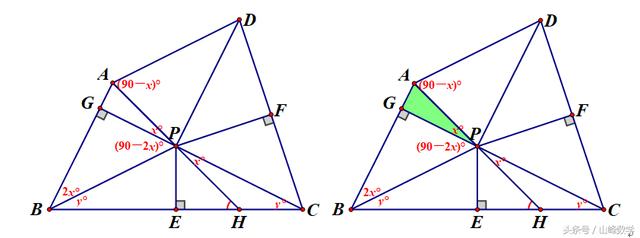
不妨假设∠AGP＝∠CPH＝x°，在Rt△APG中，可知∠PAG＝（90－x)°（如上图中绿色部分），

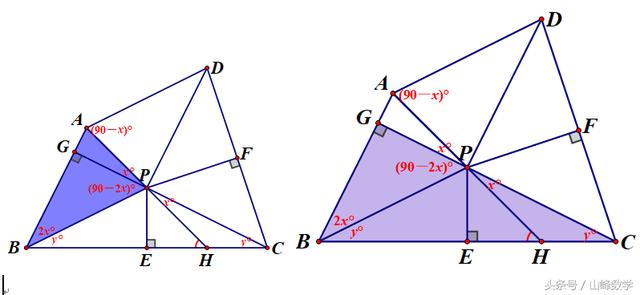
由菱形知道BA＝BP，则有∠BPA＝∠PAG＝（90－x)°，进而找出这个等腰三角形的顶角∠ABP＝2x°；由PE是中垂线可以知道∠PCB＝∠PBC＝y°，这样在Rt△BCG中两锐角和应为2(x＋y)°＝90°，从而知道(x＋y)°＝45°，如下图则可知道所求∠AHB＝45°