初中数学一题多解：一道平面几何题的十种证法

题目：如图1，△ABC中，D、F在AB上，AD=BF，过D作DE∥BC，交AC于E，过F作FG∥BC交AC于点G．求证：BC=DE＋FG．

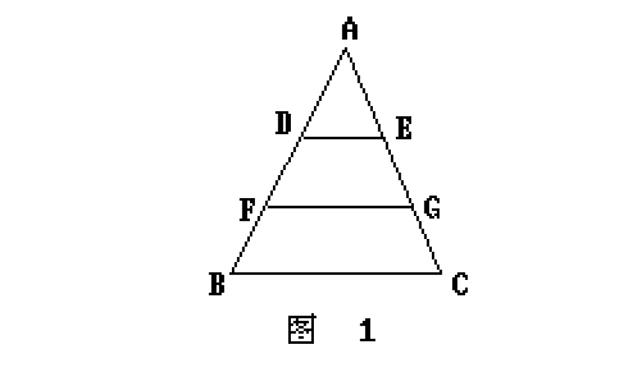
分析：证明一条线段等于另外两条线段的和，常用的方法是将线段的位置平移：

（1 ）延长较短线段与较长线段相等；

（2） 在较长线段上截取与较短线段相等的线段；

（3）将线段适当移动位置后进行比较；

（4）采用其它比较方法 ，如解析法，三角 法，面积法等．

一、延长较短线段与较长线段相等

证法1：如图2，延长FG到H，使FH等于BC，连结C H．（关键证GH=DE即可）．

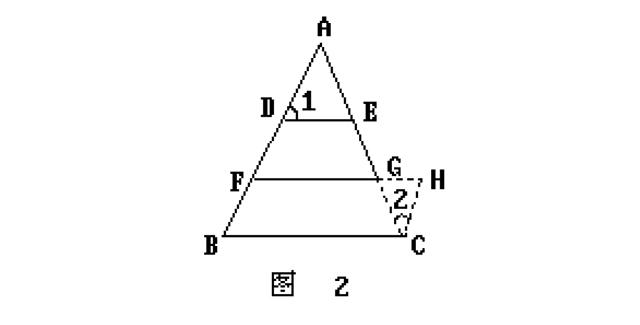
由作法知 FH平行且等于BC FBCH是平行四边形 CH=BF．

在△ADE和△CHG中，CH =BF=AD ．

由CH∥AB ∠A=∠2，又∠1=∠B，∠H=∠B，所以∠1=∠H．所以△AD E≌△CHG，则DE=GH，

故BC=FG＋GH=DE＋FG．

证法2：如图3，仍延长FG到H，使GH=DE，连结CH．

（关键证BC=FH）．

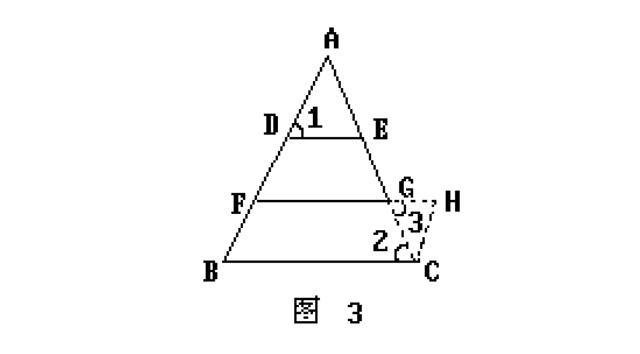
由DE∥BC∥FG ∠1=∠2=∠3．

又AD=FB，所以AE=GC．

所以△ADE≌△CHG，（SAS）

所以∠A=∠GCH AB∥CH．

所以四边形FBCH是平行四边形，所以，BC=FH，

所以BC=DE＋FG．

证法3：如图4，延长DE到H，使DH=BC，连结CH．

（关键证FG=EH）．

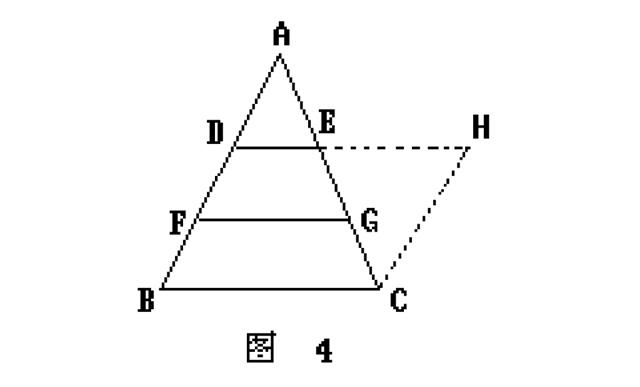
由 DBCH及DH=BC．

再△AFG≌△CHE，得FG=EH．

二、恰当地将线段平移

证法4：如图5

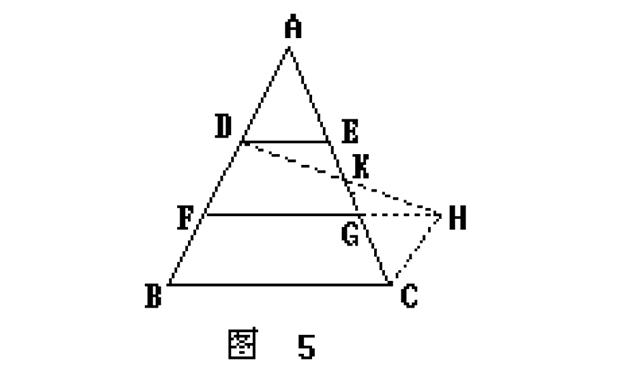
找EG的中点K，连接DK并延长DK交FG的延长线于H，可证得

△DEK≌△HGK DE=GH．

再证得 △ADE≌△CHG，（或证△ADK≌△CHK）

∴∠A=∠GCH

∴AB∥CH,FG∥BC

∴四边形FBCH是平行四边形

∴FH=BC,

所以BC=GH＋FG=DE＋FG．

证法5：如图6．

过D作DH∥AC交BC于H，则DE=HC．不难证得△AFG≌△DBH，可得FG=BH，

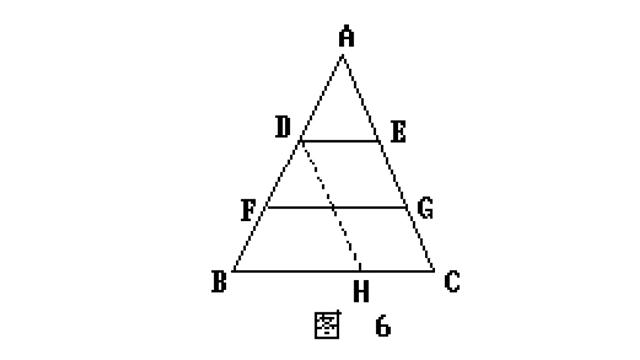
所以BC＝BH＋HC＝DE＋FG．

证法6：如图7

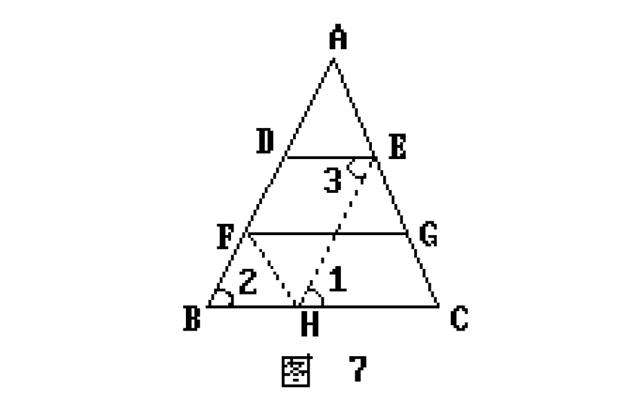
过F作FH∥AC交BC于H（或在BC上截取CH=FG）．

则得到平行四边形FHCG,平行四边形AFHE

所以，FG=HC,DE=BH

三、在较长的线段上截取较短的线段

证法7：如图8

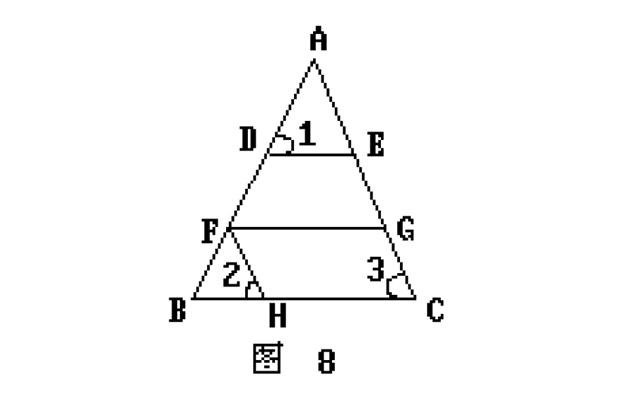
在BC上截取BH=DE．不难得出△ADE≌△FBH．则∠1=∠2=∠3 FH∥AC FG=HC．

（同理可在BC上截取BH =FG．再证HC=DE）

四、利用梯形或三角形的中位线定理

题中要证的 结论系三角形的底边BC等于梯形DFGE两底之和，可猜想通过梯形DFGE的中位线沟通两者之间的关系．

证法8：如图9．

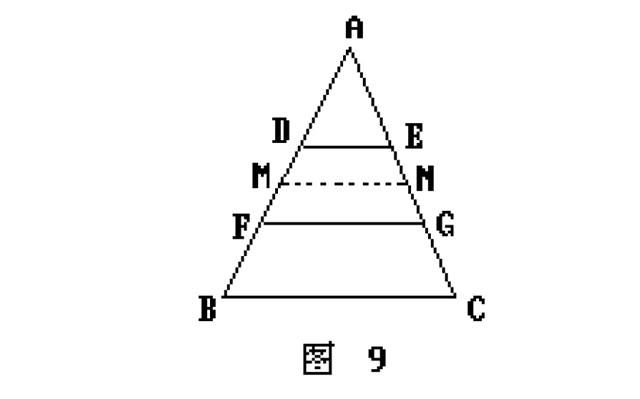
作梯形DFGE的中位线MN,则MN=(DE+FG)/2①

又AD=FB，由平行截割 定理得MN也是△ABC的中位线，

所以MN=BC/2,②

由①②知，BC=DE+FG

五、利用相似三角形的性质和比例的性质

题中要证的边实质是相似三角形的对应边，因此，可从相似三角形的对应边成比例和比例的基本性质入手证明．

证法9:如图1．

①+②得

又AD=BF，所以，AD＋AF=AD＋DB=AB．

所以

即 BC=D F＋FG．

六、其它线段变换

证法10：如图10．

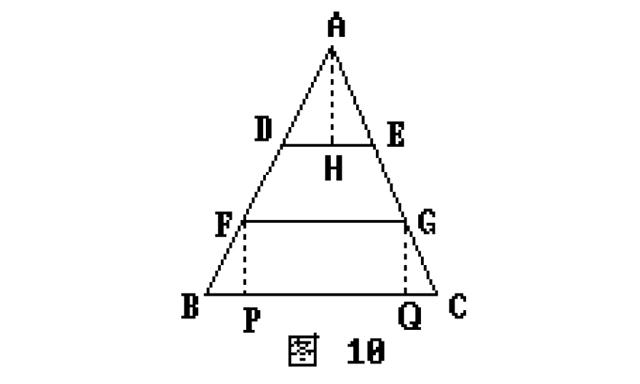
作AH⊥DE于H，作FP⊥BC于P，作GQ⊥BC于Q．易证△ADH≌△FBP，△AHE≌△GQC．

DH＋HE=BP＋QC，又FG=PQ．则 BC=PQ＋BP＋QC＝FG＋DH＋HE，即BC=DE＋FG．