4道三垂直全等模型怎么求点坐标？与平面直角坐标系有关经典考题

平面直角坐标系中，出现直角三角形（或者直角），要求某个点的坐标，怎么求？

一般规律，都是通过添加辅助线，必然出现三角形相似。当有一组对应边相等的时候，必然出全等。

现在，通过4道三角形全等的例题，总结这一类题型的解题方法。

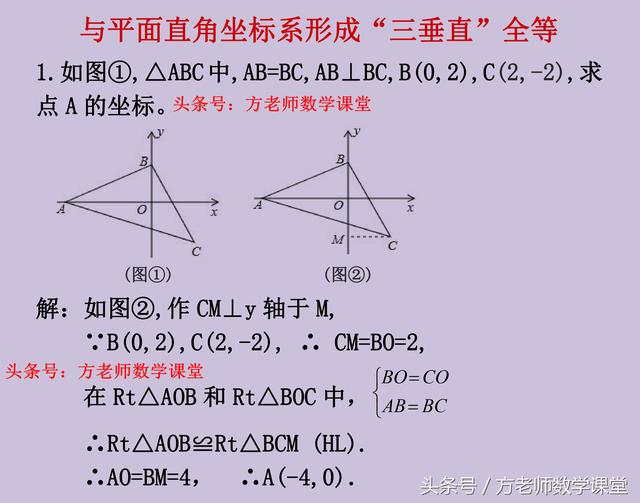
第1题、过点C作y轴的垂线，通过HL判定两个直角三角形全等。

只要熟练三角形全等的判定定理，此类题型很简单。

第2题、过点C作x轴的垂线，就是经典三垂直模型，或者叫一线三等角模型。

通过AAS，立马判定三角形全等，对应边相等，各自的线段长求出，点的坐标就出来了。

第3题、先做CD垂直X轴，再作BE垂直CD。三垂直模型，隐藏的比较深，但是辅助线一添加，就跃然纸上了。

其实，要求B点坐标，过两个点两坐标轴做垂线，也是一定的啊。你再发现三角形全等，就够了。

第4题，这个三垂直模型，添加辅助线之后，证明三角形全等是非常简单的。

最后求线段的长度，设未知数，通过直角三角形勾股定理的方法，非常巧妙。

总之，这一类题型，要求点的坐标，就一句话，就是求这个到x轴的距离，和到y轴的距离，即可。