5种常用三角形全等辅助线添加方法，有5道例题详解

cc518学习网精品学习资料总目录

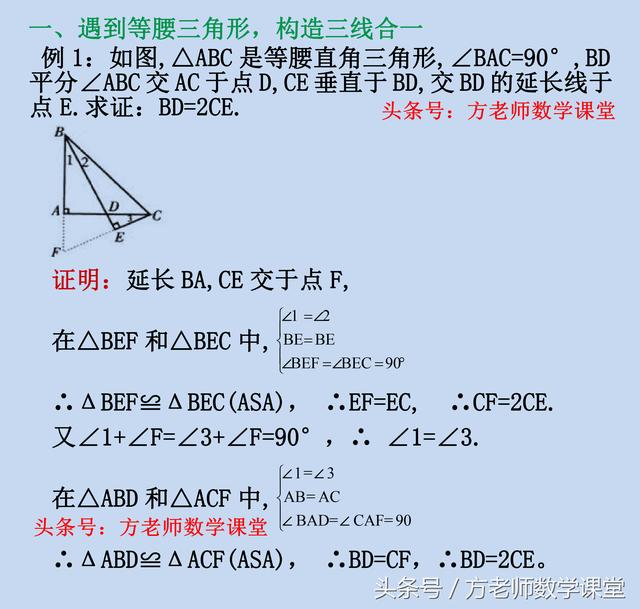
方法一、遇到等腰三角形，三线合一性质，很实用很常用。主要思维模式，就是利用三角形全等变换中的对折。

等腰三角形的三线合一的性质，在三角形的辅助线添加中应用非常广泛，同学们可以多多总结。

方法二、有三角形中线，倍长中线，构造三角形全等。这个方法，是基本方法，屡试屡爽。是利用三角形全等转换中的旋转。

本来有中点，两线段相等。再倍长中线，得两线段相等。再对顶角相等。所以，三角形全等秒出。

方法三、遇见角平分线，做双垂直，必出三角形全等。可以从角平分线上的点向两边做垂直，也可以过角平分线上的点做角平分线的垂直与角的两边相交。

这个方法，利用了三角形全等变换中的对折性质。在很多综合几何题当中，角平分线的这个辅助线添加方法也很实用。

方法四。根据题意，做平行线，比如例4中，过点E做EG∥AC。此刻，这个问题，就迎刃而解了。

做平行线的方法也特别实用，主要利用了三角形全等变换中的平移，或者翻转折叠思想。同学平时多总结类似的题型，和解题方法。

五。截长补短法，得三角形全等。这个方法，之前方老师还发过一个关于截长不补短发的专题内容。

一般来说，遇见求证一条线段等于两条线段之后的时候，多需用到截长或补短法，来添加辅助线。