明“因”熟“力”，破解平衡问题（2）

9.某装置如图所示，两根长度均为l的轻杆OA、OB与质量均为m的小球及一小滑块通过铰链连接，杆OA的A端与固定在竖直光滑杆上的铰链相连。原长也为l的轻质弹簧一端固定在A点，另一端连接小滑块，弹簧与小滑块都套在竖直杆上，装置静止时，弹簧长为1.6l，重力加速度为g，下列说法正确的是( )

A．杆OA对小球的作用力方向与竖直杆的夹角为53°

B．杆OB对小滑块的作用力方向沿杆OB向下，大小为8(5mg)

C．杆OA与OB对小球的作用力大小之比为3(4)

D．弹簧的劲度系数为2l(5mg)

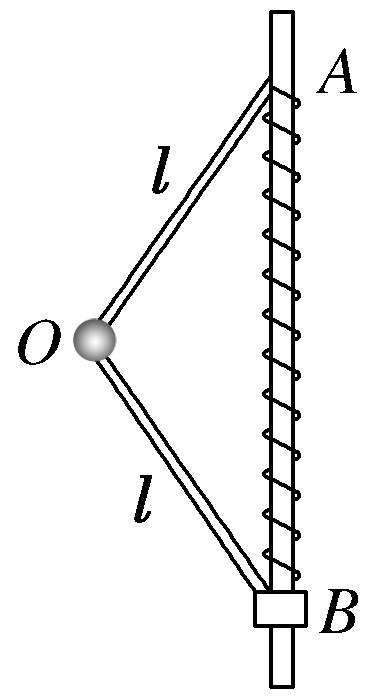
解析：选BD　对小球受力分析如图所示，受重力、杆OA、OB对小球的支持力(沿着杆的方向)，结合几何关系与三角知识，则有：设杆OA与竖直杆的夹角为θ，cos θ＝2()，解得：θ＝37°，因FA＝FB，杆OA与OB对小球的作用力大小之比是1∶1，故A、C错误；对小滑块受力分析如图所示；由上述分析可知，FB＝2()＝8(5mg)，由牛顿第三定律，则杆OB对小滑块的作用力方向沿杆OB向下，大小为8(5mg)，故B正确；对于小滑块，根据平衡条件，则有：＝mg＋8(5mg)cos 37°＝2(3)mg，由胡克定律，则有弹簧的劲度系数：k＝1.6l－l(T)＝2l(5mg)，故D正确。

二、非选择题

10．如图所示，

一质量为M＝2 kg的铁块套在倾斜放置的杆上，杆与水平方向的夹角θ＝60°，一轻绳一端连在铁块上，一端连在一质量为m＝1 kg的小球上，一水平力F作用在小球上，连接铁块与球的轻绳与杆垂直，铁块和球都处于静止状态。(g取10 m/s2)求：

(1)拉力F的大小。

(2)杆对铁块的摩擦力的大小。

解析：(1)

对B受力分析，由平衡条件知FTsin θ＝F

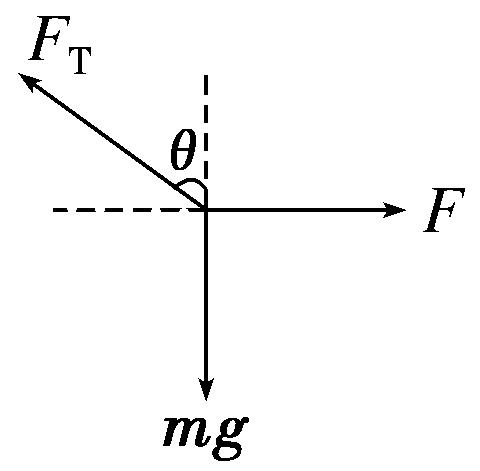
FTcos θ＝mg

解得F＝mgtan θ＝10 N。

(2)对A受力分析，有

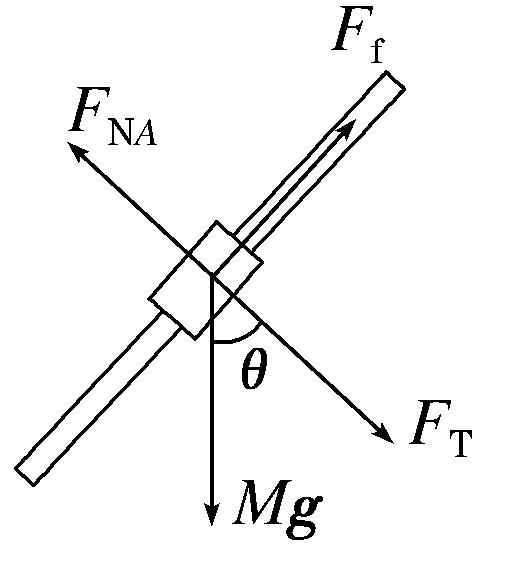
Ff＝Mgsin θ＝10 N。

答案：(1)10 N　(2)10 N

11．一足够长的轻绳跨过两个等高的轻定滑轮(大小和摩擦不计)，两端分别挂上质量为m1＝4 kg和m2＝2 kg的物体，如图所示，在滑轮之间的绳上通过死结悬挂质量为m的物体，为使三物体保持平衡，求m的取值范围。

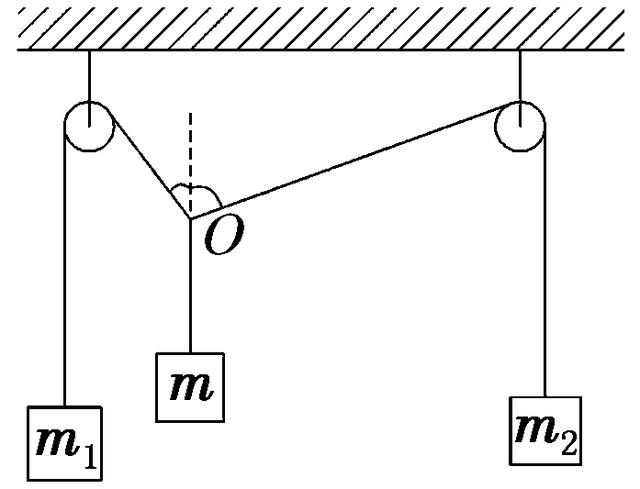
解析：平衡时，O点受力如图所示，由物体的平衡条件易知

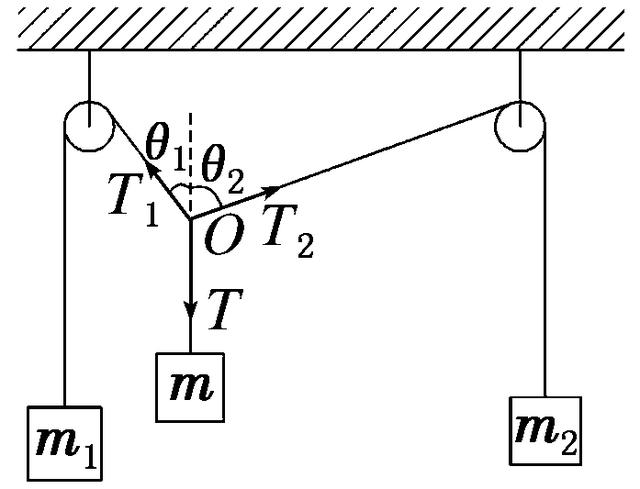
T1cos θ1＋T2cos θ2＝T＝mg

T1sin θ1＝T2sin θ2

将T1＝m1g＝40 N，

T2＝m2g＝20 N代入得：

4cos θ1＋2cos θ2＝m,2sin θ1＝sin θ2

所以m＝4 sin2θ2(1)＋2cos θ2，进行如下讨论：

当θ2＝0时，m最大mmax＝6 kg，

当θ2＝90°，m最小mmin＝2 kg。

因为θ2＝0、θ2＝90°时取不到，

故三物体平衡时，

m的取值范围是2 kg<m<6 kg。

答案：2 kg<m<6 kg