“一模”“两路”“三角”“两难点”，破解天体运动问题（1）

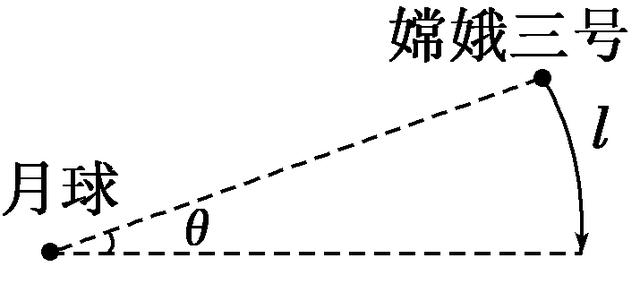
1.如图所示，“嫦娥三号”的环月轨道可近似看成是圆轨道，观察“嫦娥三号”在环月轨道上的运动，发现每经过时间t通过的弧长为l，该弧长对应的圆心角为θ弧度。已知万有引力常量为G，则月球的质量是( )

A.Gθ3t(l2) B.Gl2t(θ)

C.Gθt2(l3) D.Gθl3(t2)

解析：选C　设“嫦娥三号”做圆周运动的角速度为ω，则Gr2(Mm)＝mω2r，又l＝rθ，ω＝t(θ)，联立得月球的质量M＝Gθt2(l3)，故C正确。

2．(2016·四川高考)国务院批复，自2016年起将4月24日设立为“中国航天日”。1970年4月24日我国首次成功发射的人造卫星东方红一号，目前仍然在椭圆轨道上运行，其轨道近地点高度约为440 km，远地点高度约为2 060 km；1984年4月8日成功发射的东方红二号卫星运行在赤道上空35 786 km的地球同步轨道上。设东方红一号在远地点的加速度为a1，东方红二号的加速度为a2，固定在地球赤道上的物体随地球自转的加速度为a3，则a1、a2、a3的大小关系为( )

A．a2＞a1＞a3 B．a3＞a2＞a1

C．a3＞a1＞a2 D．a1＞a2＞a3

解析：选D　卫星围绕地球运行时，万有引力提供向心力，对于东方红一号，在远地点时有G(R＋h1)2(Mm1)＝m1a1，即a1＝(R＋h1)2(GM)，对于东方红二号，有G(R＋h2)2(Mm2)＝m2a2，即a2＝(R＋h2)2(GM)，由于h2＞h1，故a1＞a2，东方红二号卫星与地球自转的角速度相等，由于东方红二号做圆周运动的轨道半径大于地球赤道上物体做圆周运动的半径，根据a＝ω2r，故a2＞a3，所以a1＞a2＞a3，选项D正确，A、B、C错误。

3.

(2017·淮安模拟)一颗卫星绕地球沿椭圆轨道运动，A、B是卫星运动的远地点和近地点。下列说法中正确的是( )

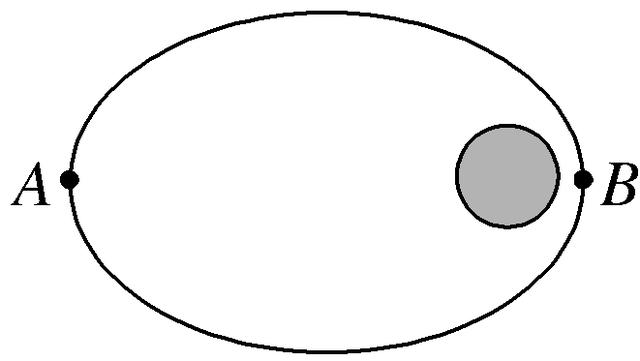
A．卫星在A点的角速度大于B点的角速度

B．卫星在A点的加速度小于B点的加速度

C．卫星由A运动到B过程中动能减小，势能增加

D．卫星由A运动到B过程中引力做正功，机械能增大

解析：选B　近地点的速度较大，可知B点的线速度大于A点的线速度，根据ω＝r(v)知，卫星在A点的角速度小于B点的角速度，故A错误；根据牛顿第二定律得，a＝m(F)＝r2(GM)，可知卫星在A点的加速度小于B点的加速度，故B正确；卫星沿椭圆轨道运动，从A到B，万有引力做正功，动能增加，势能减小，机械能守恒，故C、D错误。

4．双星系统由两颗恒星组成，两恒星在相互引力的作用下，分别围绕其连线上的某一点做周期相同的匀速圆周运动。研究发现，双星系统演化过程中，两星的总质量、距离和周期均可能发生变化。若某双星系统中两星做圆周运动的周期为T，经过一段时间演化后，两星总质量变为原来的k倍，两星之间的距离变为原来的n倍，则此时圆周运动的周期为( )

A.k2(n3)T B.k(n3)T

C.k(n2)T D.k(n)T

解析：选B　设两恒星的质量分别为M1和M2，轨道半径分别为r1和r2。根据万有引力定律及牛顿第二定律可得r2(GM1M2)＝M1T(2π)2r1＝M2T(2π)2r2，解得r2(G(M1＋M2))＝T(2π)2(r1＋r2)，即r3(GM)＝T(2π)2①，当两星的总质量变为原来的k倍，它们之间的距离变为原来的n倍时，有(nr)3(GkM)＝T′(2π)2②，联立①②两式可得T′＝ k(n3)T，故B项正确。

5．2016年9月15日，中国成功发射天宫二号空间实验室，对其轨道进行控制、调整到距离地面高h＝393 km处与随后发射的神舟11号飞船成功对接，景海鹏和陈冬雨两名航天员进驻天宫二号。已知地球半径为R，地球表面重力加速度为g，当天宫二号在预定轨道正常运行时，下列描述正确的是( )

A．宇航员在天宫二号内可用天平测物体的质量

B．天宫二号运动周期大于24 h

C．天宫二号线速度大小为

D．天宫二号如果要变轨到高轨道则需要加速

解析：选D　天平是根据杠杆平衡原理制成的，在天宫二号中，物体和砝码所受重力完全提供向心力，天平的左右两盘无论放多少物体，天平都是平衡的，所以无法用天平测量物体的质量，即不能使用，故A错误；天宫二号的轨道半径小于地球同步卫星的轨道半径，根据Gr2(Mm)＝mT2(4π2r) 可知T＝2πGM(r3)，半径越大，周期越大，所以天宫二号运动周期小于24 h，故B错误；根据G(R＋h)2(Mm)＝mR＋h(v2)以及GR2(Mm)＝mg得：v＝R＋h(gR2)，故C错误；天宫二号如果要变轨到高轨道，需要做离心运动，需要的向心力大于万有引力，所以要加速，故D正确。