中考数学动点线段和差最值问题，逃不出这三种题型

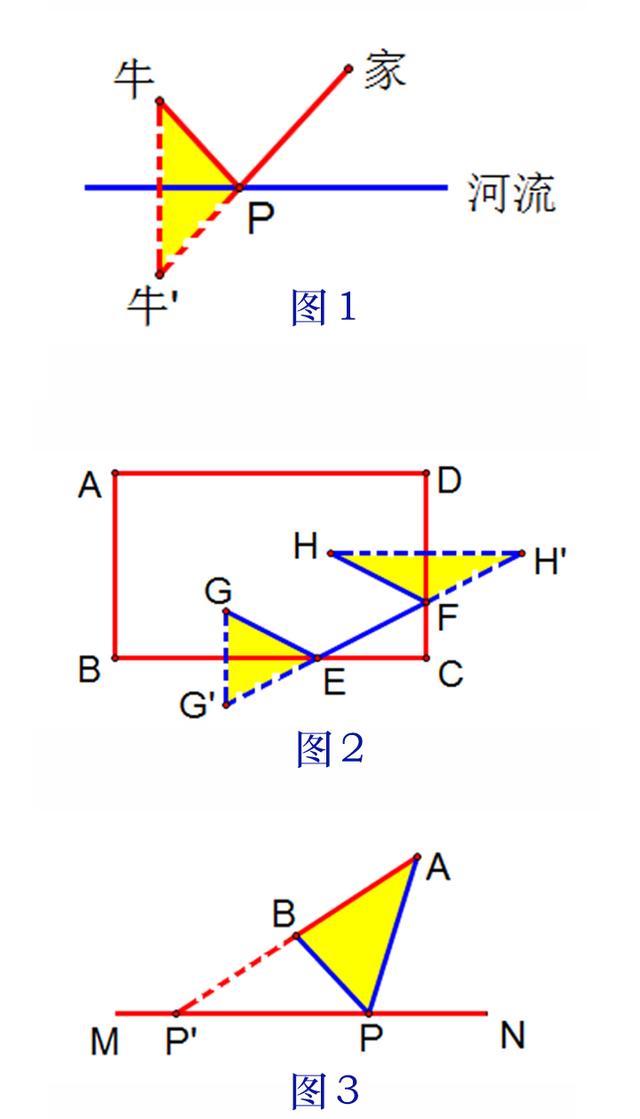
两条动线段的和的最小值问题，常见的是典型的“牛喝水”问题，关键是指出一条对称轴“河流”（如图1）．

三条动线段的和的最小值问题，常见的是典型的“台球两次碰壁”或“光的两次反射”问题，关键是指出两条对称轴“反射镜面”（如图2）．

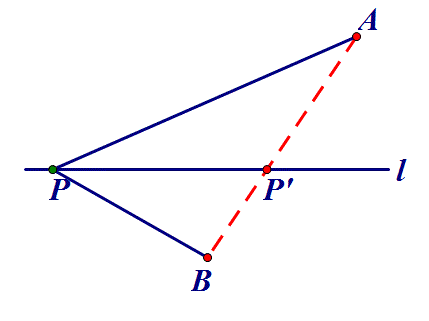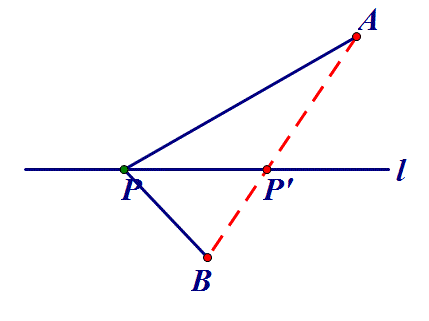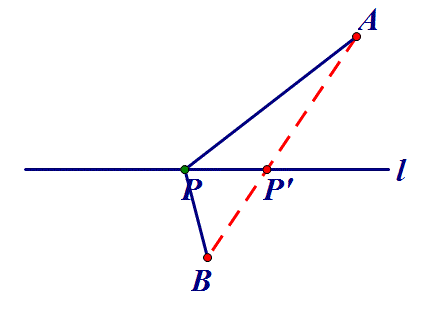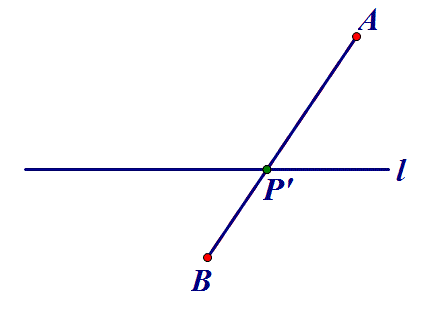
两条线段差的最大值问题，一般根据三角形的两边之差小于第三边，当三点共线时，两条线段差的最大值就是第三边的长．如图3，PA与PB的差的最大值就是AB，此时点P在AB的延长线上，即P′．

解决线段和差的最值问题，有时候求函数的最值更方便，本讲不涉及函数最值问题．

【例题解析】：

例1、如图1-1，抛物线y＝x²－2x－3与x轴交于A、B两点，与y轴交于点C，点P是抛物线对称轴上的一个动点，如果△PAC的周长最小，求点P的坐标．

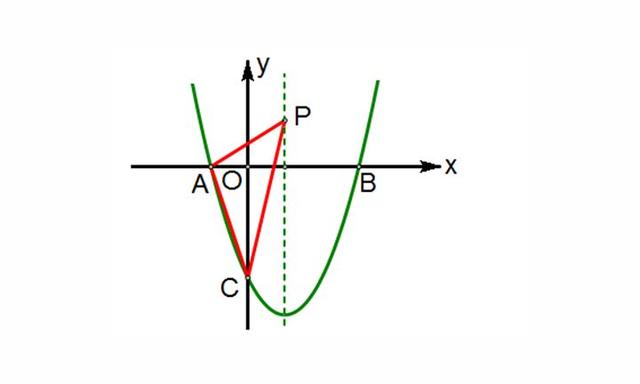
图1-1

【解析】如图1-2，把抛物线的对称轴当作河流，点A与点B对称，连结BC，那么在△PBC中，PB＋PC总是大于BC的．如图1-3，当点P落在BC上时， PB＋PC最小，因此PA＋PC最小，△ PAC的周长也最小．

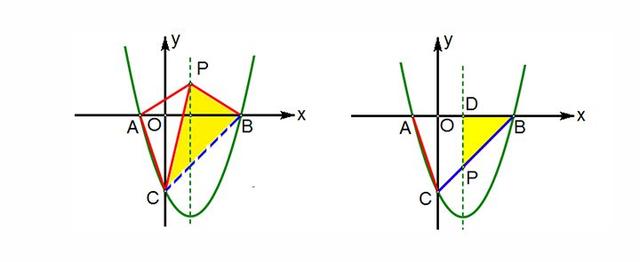
图1-2

由y＝x²－2x－3，可知OB＝OC＝3，OD＝1．所以DB＝DP＝2，因此P(1,－2)．

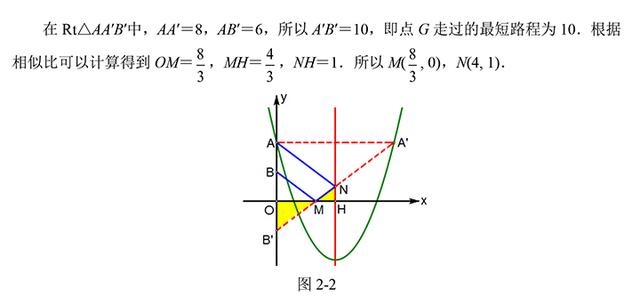
例2、如图，抛物线y＝x²/2－4x+4与y轴交于点A，B是OA的中点．一个动点G从点B出发，先经过x轴上的点M，再经过抛物线对称轴上的点N，然后返回到点A．如果动点G走过的路程最短，请找出点M、N的位置，并求最短路程．

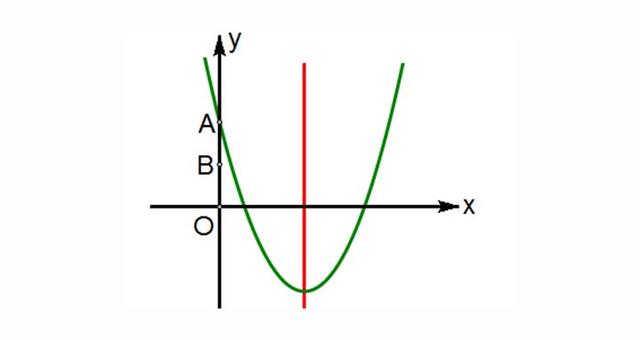
图2-1

【解析】如图2-2，按照“台球两次碰壁”的模型，作点A关于抛物线的对称轴对称的点A′，作点B关于x轴对称的点B′，连结A′B′与x轴交于点M，与抛物线的对称轴交于点N．

【知识总结】：

对于线段最值问题一般转化以下三种类型：

1、定点到定点→连线段：点P在直线l上，AP+BP何时最小？

2、定点到定线→做垂线：点P在直线l上，AP何时最小？

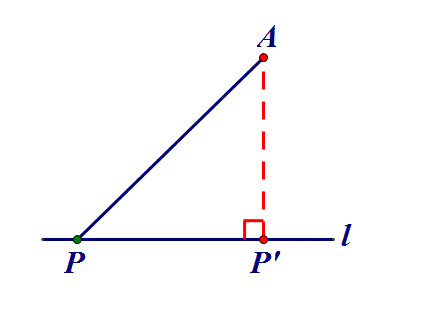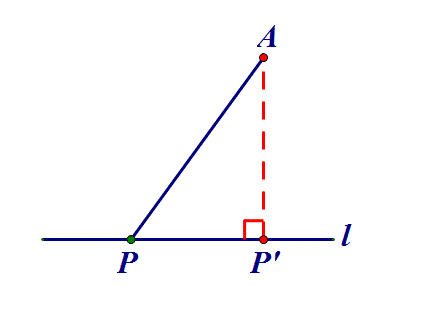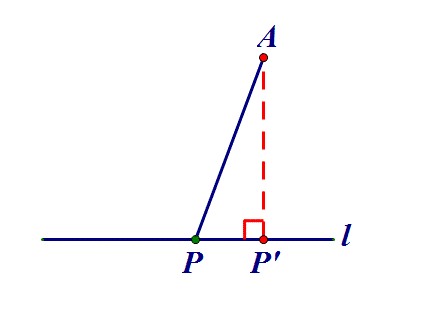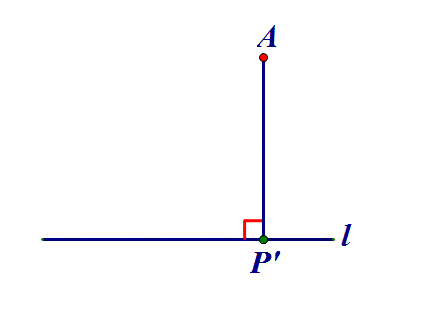
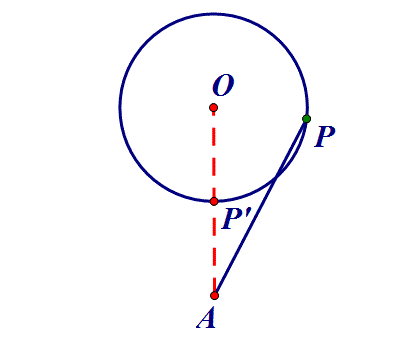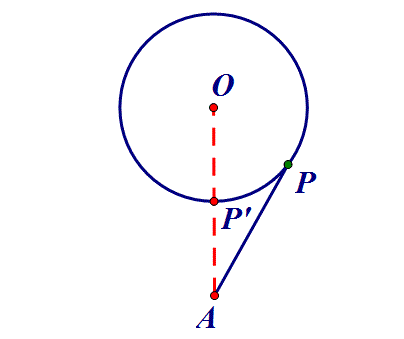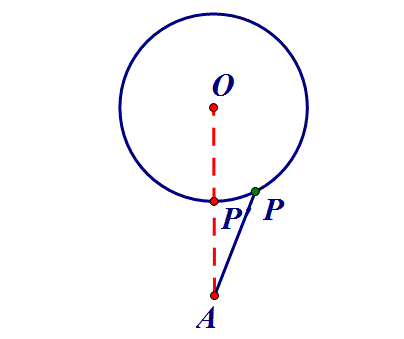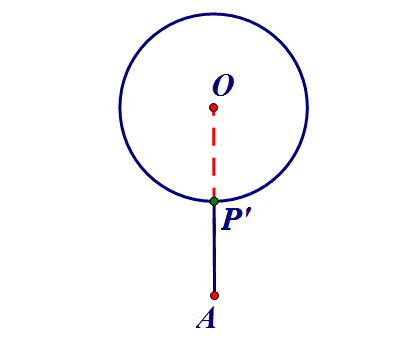
3、定点到定圆→连心线：点P在圆O上，AP何时最小？

对于线段和差最值的问题，跑不出这三种类型。希望大家牢记此类方法。