初中数学：三角形易错点突破和重难点解析

易错点突破

1．运用三角形三边关系性质致误

例1、若等腰三角形的一条边长为6厘米，另一边长为2厘米，则它的周长为（ ）.

A．10厘米 B．14厘米 C．10厘米或14厘米 D．无法确定

错解：由于本题未指明所给边长是等腰三角形的腰还是底，所以需讨论：①当腰长为6厘米时，底边长为2厘米，则周长为6+6+2=14（cm）；②当腰长为2厘米时，底边长为6厘米，则周长为6+2+2=10（cm）. 故选C.

分析：本题错在没有注意到三角形成立的条件：“三角形的任意两边之和大于第 三边”，当腰长为2厘米，底边长为6厘米时，不能构成三角形.

正解：本题只能把6厘米作为腰，2厘米作为底，故三角形的周长为14厘米，故选B.

2．应用判定方法致误

例2、如图3，已知AB=DC，OA=OD，∠A=∠D. 问∠1=∠2吗？试说明理由.

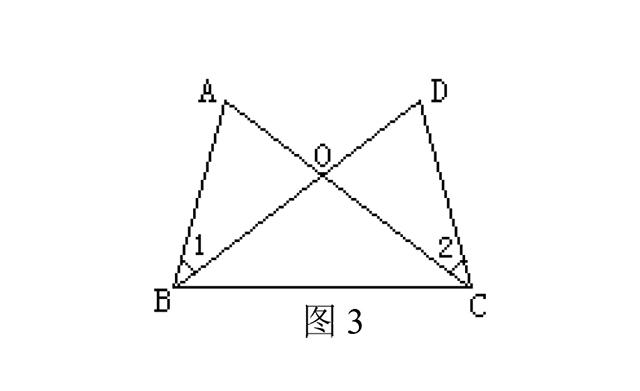
错解：∠1=∠2. 理由如下：

在△AOB和△DOC中，因为AB=DC，OA=OD，∠AOB=∠DOC，

所以△AOB≌△DOC，所以∠1=∠2.

分析：不存在“角角角（AAA）”和“边边角（SSA）”的判定方法，即对于一般三 角形，“有三个角对应相等的两个三角形不一定全等”和“有两边和其中一边的对角对应相等的两个三角形不一定 全等.”

正解：在△AOB和△DOC中，因为AB=DC，∠A=∠D，OA=OD，

所以△AO B≌△DOC（SAS），所以∠1=∠2.

3．不理解“对应”致误

例3、已知在两个直角三角形中，有一对锐角相等，又有一组边相等，那么这两个三角形是否全等？

错解：这两个三角形全等.

分析：对“ASA”全等判定法中“对应边相等”没有理解，错把边相等当成对应边相等.

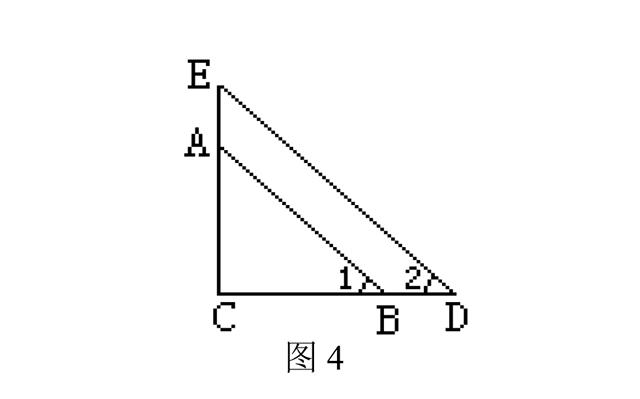
正解：这两个三角形不一定全等. 如图4所示，在RT△EDC中，∠1=∠2，CD=AB，∠C=∠C=90°，显然△ABC和△EDC不全等.

重难点析解

1．三角形的有关概念

例1能把一个三角形分成面积相等的两部分的是该三角形的一条（ ）

A．中线 B．角平分线 C．高线 D．边的垂直平分线

分析：根据 三角形中线的特征及其面积公式可知，等底同高的两三角形的面积相等.

解：只有三角形的一条中线才能把三角形的面积分成相等的两部分. 故选A.

评注：三角形的“三线”在解题中有着广泛的应用，因此，要正确认识其定义及特征.

2．三角形的三边之间的关系

例2下列长度的三条线段，能组成三角形的是（ ）.

A．1厘米，2 厘米，3厘米 B．2厘米，3 厘米，6 厘米

C．4厘米，6 厘米，8厘米 D．5厘米，6 厘米，12厘米

分析：判断三条线段能否构成三角形，只需检验两条较短的线段之和是否大于最长线段即可，若大于则能构成，否则不能构成.

解：根据“三角形 的两边之和大于第三边”.然后观察四个选项，满足两边之和大于第三边的只有4厘米，6 厘米，8厘米. 故选C.

评注：涉及三角形三边关系的问题时，应注意三角形三边关系的应用.

3.三角形的内角和

例3、如图5，∠1=100°，∠2=145°，那么∠3的度数是（ ）.

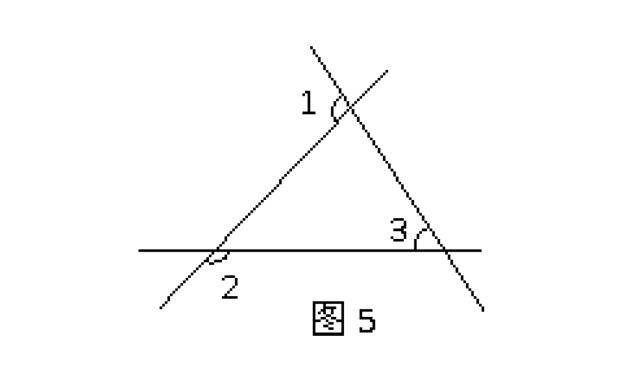
A．55° B．65° C．75° D．85°

分析：本题 可利用平角及邻补角的定义，把 和 转化为三角形的内角.

解：由图5可知：与∠1相邻的补角为80°，与∠2相邻的补角为35°，由三角形的内角和为180°，可得∠3=180°-80°-35°=65° . 故选B.

评注：涉及三角形有关的角度计算问题，一般要考虑到三角形内角和的应用.

4．全等三角形的性质

例4、如图6，已知AB=AD，AC=AE ，∠1=∠2 .试说明BC=DE.

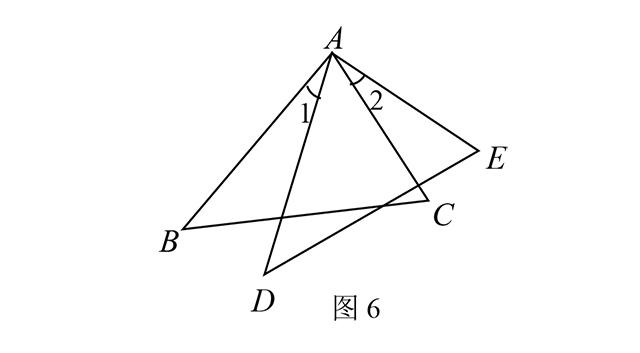
分析：要说明BC=DE，只要说明△ABC≌△ADE即可. 由已知条件可知，这两个三角形已经具备两边对应相等，因此再找这两边的夹角相等即可.

解：因为∠1=∠2，所以∠1+∠DAC=∠2+∠DAC，即∠BAC=∠DAE .

又因为AB=AD，AC=AE，所以△ABC≌△ADE（SAS），所以BC=DE .

评注：因为全等三角形的对应边相等，所以要说明分别属于两个三角形的线段相等，常常通过说明这两个三角形全等来解决问题.

5．利用三角形全等解决实际问题

例5、如图7，A，B，C，D是四个村庄，B，D，C在一条东西走向公路的沿线上，BD=1千米，DC=1千米，村庄AC、AD间也有公路相连，且AD⊥ BC，AC=3千米，只有村庄AB之间由于间隔了一个小湖，所以无直接相连的公路. 现准备在湖面上造一座斜拉桥，测得AE=1.2千米，BF=0.7千米. 试求所建造的斜拉桥长有多少千米？

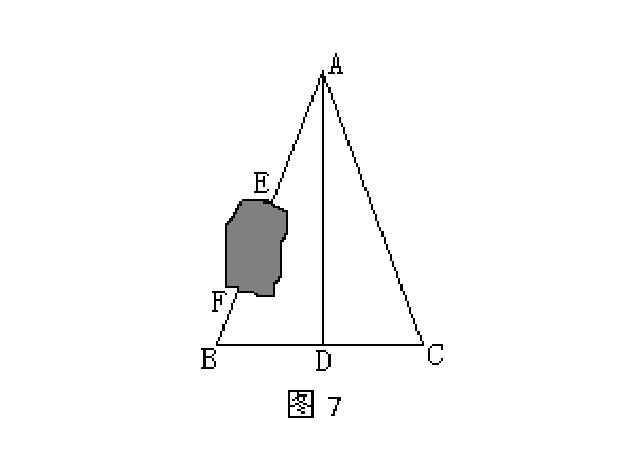
分析：由于村庄AB之间间隔了一个小湖，无法直接测量，故可利用转化思想，由△ADB≌△ADC，得AB=AC=3千米，从而计算出EF的长.

解：在△ADB和△ADC中，因为BD=DC，∠ADB=∠ADC=90°，AD=AD，

所以△ADB≌△ADC（SAS）.所以AB=AC=3千米.

所以EF=AB-(AE+BF)=3-(1.2+0.7)=1.1（千米）.

评注：三角形全等是证明线段、角相等的重要依据，教材中全等三角形的例题、习题有很多是与生活息息相关的，其基本思路是通过建立数学模型，把实际问题先转化为数学问题.