一线三等角模型
学习目标:用“一线三等角”基本模型,解决全等三角形、相似三角形中的相关问题
重点:掌握“一线三等角”基本模型
难点:“一线三等角”基本模型的提炼、变式和运用
所谓“一线三等角”,通俗地讲就是一条直线上有三个相等的角,一般就会存在相似三角形,当对应边也相等时,就会有全等三角形,即:“一线三等角,全等相似两边找”
看一下它的基本模型:
锐角型:
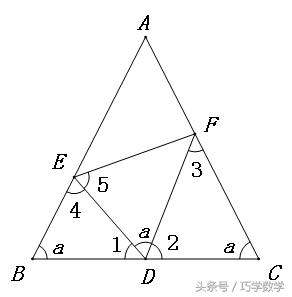
如图,等腰△ABC中,∠DEF=∠B=∠C,图中有没有相似三角形?请说明理由。
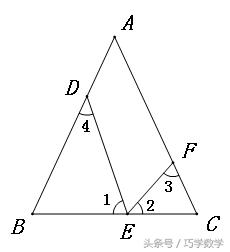
∵∠1+∠4=180°-∠B,∠1+∠2=180°-∠DEF
∠B=∠DEF
∴∠2=∠4
又∵∠B=∠C
∴△BDE∽△CEF
钝角型:
如图,四边形ABCD中,∠DEC=∠A=∠B,找出图中相似三角形并证明。
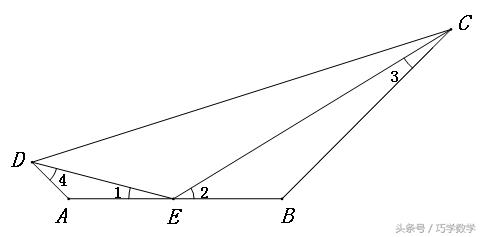
∵∠1+∠4=180°-∠A,∠1+∠2=180°-∠DEC
∠A=∠DEC
∴∠2=∠4
又∵∠A=∠B
∴△ADE∽△BEC
直角型:
如图,A、B、C三点共线,∠A=∠C=∠DBE=90°,用同样的方法,易证△ABD∽△CEB,直角型的三垂直我们又把它叫做“三垂直模型”,它的应用更加广泛,考试出现的概率最大
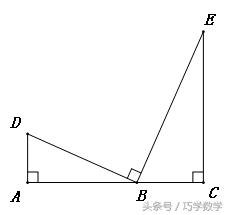
全等型:
如图,B、C、D三点共线,∠B=∠D=∠ACE,AB=CD,求证△ABC≌△CDE.
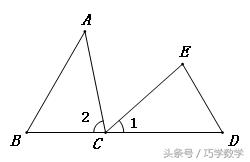
由一线三等角,易证∠1=∠A
又∵AB=CD,∠B=∠D
∴△ABC≌△CDE(ASA)
由以上基本模型发现,一线三等角模型中,一定存在相似三角形,有可能存在全等三角形(全等是相似的一种特殊情况)
中点型“一线三等角”模型
如图,等腰三角形ABC中,AB=AC,∠EDF=∠B,D是BC边的中点,请找出图中所有的相似三角形,并证明。

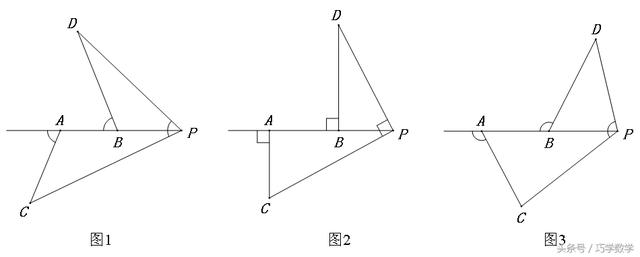
我们通过观察发现,以上“一线三等角模型”有个共同点,三个角均在直线的同一侧,当这三个角不在同一侧时,会有相似三角形存在吗?如下图,自己找出相似三角形并证明。
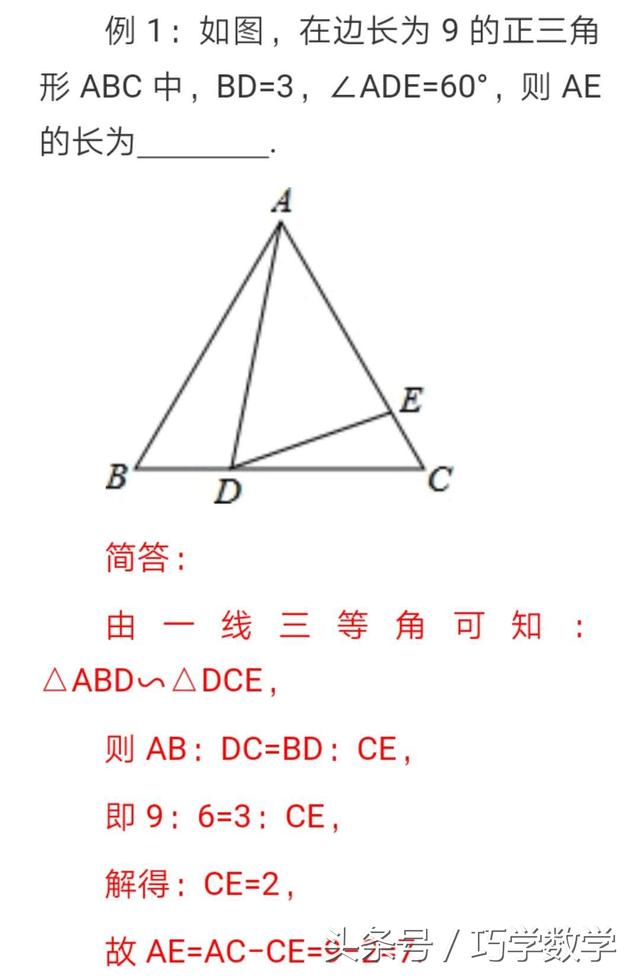
典型例题:
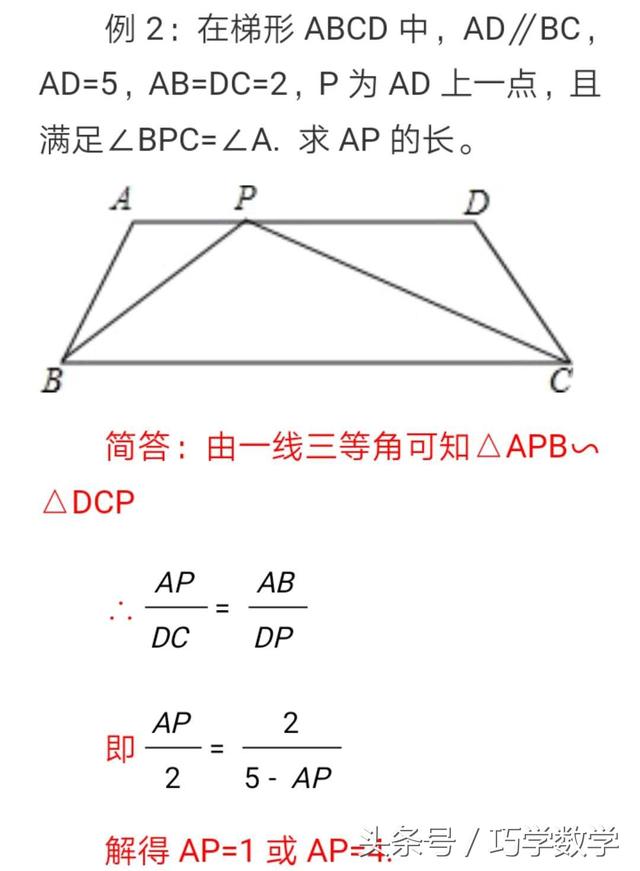
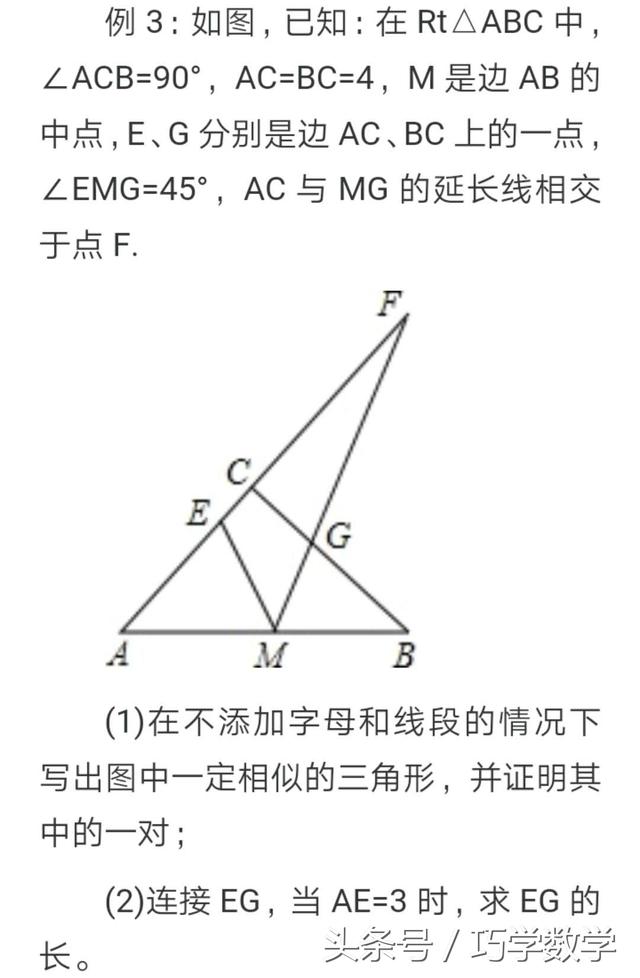


 加载中,请稍侯......
加载中,请稍侯......
精彩评论