「高中数学」一道三角函数最值问题的解法分析

题目：

若在△ABC中，∠A=60°，a=1，求三角形周长l的取值范围。

解析：题目已知一角和其对边，让求b+c的取值范围，很容易联想到正弦定理，即利用正弦定理用∠B和∠C的正弦值表示出b+c，然后再将两个角转化为一个角，利用三角函数有界性来解，思路很清晰，过程如下：

方法一：三角函数有界性法

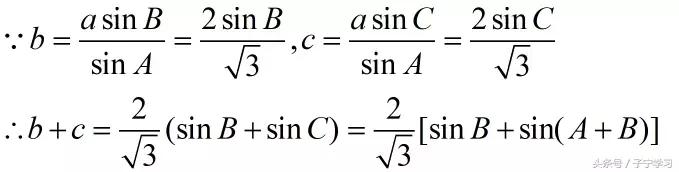
省略中间计算过程，整理得到

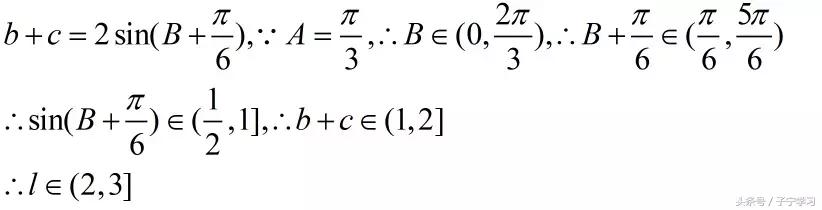
有界性方法评价：简单直接，直接可求得最大最小值，缺点是计算过程繁琐，如果化简时利用辅助角公式无法求出准确的φ值，则此方法求的的最值可能会出现错误。

方法二：函数法

这里的函数法是属于整体换元法的一种，即需要有所换元的部分，也要有等式，题目中求b+c可以当成可换元的部分，题目中与边长有关的等式为余弦定理，过程如下：

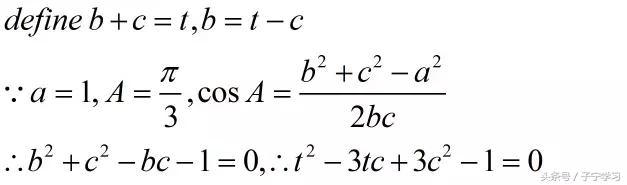
注意我们需要求的是t的范围，求哪个，哪个就不是未知数，因此变形为：3c²-3tc+t²-1=0

要保证关于c的二次等式成立了，则需要满足判别式≥0，即4-t²≥0，解得t≤2，此时可求出最大值，关于最小值可利用三角形三边关系，即b+c>a,所以b+c>1,因此可得周长的取值范围为(2,3]。

此方法计算量不太大，但是有缺陷，如果求的是b+2c的取值范围，则无法求出最小值，只能求出最大值

方法三：不等式法

求b+c的取值范围，若直接利用均值不等式，则需要出现定值，且和有最小值，因为我们可以直接利用三边关系求出最小值，因此若求最大值，则需要从一个等式入手，利用不等关系求出b+c的最大值，不等关系依旧是余弦定理，过程如下：

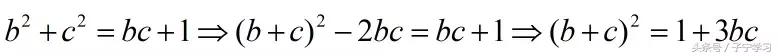
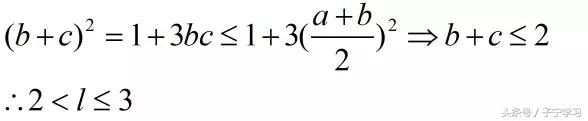
这种方法依旧无法克服若求b+2c最值的情况，计算简单，但是也有局限性。

以上即为解三角形中最常用的三种最值求法，可以看出没有一种方法是全能的，在具体解题过程中万不可死记硬背题型的方法，若只是与边有关的最大值问题中，函数法是一个相对于其他两种方法更有效的方法，推荐同学们掌握使用。