写在前面
分式方程作为中考计算题的常考类型,还是非常重要的,许多同学对于增根,无解的概念还是十分模糊,容易混淆,因此本讲就重点从增根的产生开始,详细讲解三类分式提高题.
一、分式方程无解的两种情况
例1

分析:
x=2是原方程的解吗?
不是!当x=2时,恰好使原分式方程中的分母等于0,从而使分式方程无意义.这样的根就叫做原分式方程的增根.
那么,解分式方程产生增根的原因是什么呢?
增根的产生是在解分式方程的第一步“去分母”时造成的,这一步必须满足方程的两边都乘(或除以)的是同一个不为0的数.而当x=2时,相当于原分式方程的两边都乘的数是0,那么变形前后的方程就不是同解方程了.
说得再直观些,比如方程2x=4,两边同乘0,变成了0x=0,前者只有一个解,后者有无数解,就不是同解方程.
因此,上面求得的根只能是原方程的增根.由此可知,增根有两条重要性质:
1、增根是去分母后所得整式方程的根.
2、增根使最简公分母等于0.
由此,我们应该在解出分式方程后,作必不可少的一步工作,那就是检验.
经检验,x=2是增根,
原方程无解.
例2

分析:
此方程化为整式方程后,本身就无解,当然原分式方程肯定就无解了.
由此可见,分式方程无解不一定就是产生增根.
应该共包含两种情形:
(1)原方程去分母后的整式方程有解,但这个解使原方程的最简公分母为0,是原分式方程的增根,从而原方程无解.
(2)原方程去分母后的整式方程出现0x=b(b≠0)的形式,此时整式方程无解,原方程也无解.
二、增根,无解,有范围典型题3类
(1)含参方程有增根
例1
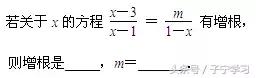
分析:
分式方程有增根,说明同乘的最简公分母为0,即可确定增根.而要求参数,则必须先解分式方程,去分母转化为整式方程,用含参数的代数式表示未知数,把是增根的未知数的值再代入,即可求出参数.
解答:
x-1=0,增根是x=1
两边同乘(x-1)得,
x-3=-m,
x=3-m,当x=1时,m=2
变式

分析:
由题意,可知最简公分母为(x+2)(x-2),则增根的值有2个,将其化成整式方程后,应该将两个值都代入.
解答:
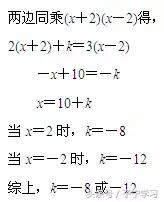
(2)含参方程无解
例2
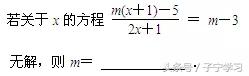
分析:
前文提到,分式方程无解,无非两种情况:(1)整式方程的解是增根(2)整式方程无解.
因此,必须把两种情况都考虑在内.
解答:

变式
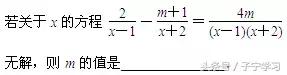
分析:
考虑两种情况,在考虑是增根的情况下,应该注意增根是两个.
解答:

(3)含参方程的解有范围
例3

分析:
显然,还是要先把分式方程转化为整式方程求解,用含参数的代数式表示未知数,根据解的范围,建立含参数的不等式,求出参数的范围.
但这里尤其值得注意的是,未知数不能是增根,即含参数的代数式的值不能等于增根的值.
解答:

变式
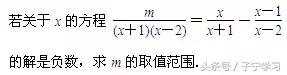
分析:
方法同上,注意增根有2个.
解答:

小结
以上3种例题,相信同学们都看懂了,到了总结归纳的时候了.
一、分式方程有增根方法总结:
(1)化为整式方程.
(2)确定增根.
(3)把增根代入整式方程求出字母参数的值.
二、分式方程无解方法总结:
(1)化为整式方程.(可能含字母参数为系数)
(2)把增根代入整式方程,求出字母参数的值.
(3)整式方程无解,则含字母参数的系数为0,求出字母参数的值.
三、分式方程的解有范围方法总结:
(1)化为整式方程.(可能含字母参数为系数)
(2)用含字母参数的代数式表示未知数,解不等式.
(3)把增根代入整式方程,求出字母参数不能取的值.
三、分式方程提高题两类
(1)待定系数法的运用
例1
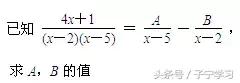
分析:
本题既可以从通分的角度来看,也可以从解分式方程入手,得到4x+1与含参数A,B的代数式相等的一个等式,继而利用待定系数法,这个代数式的一次项系数是4,常数项是1,得到关于A,B的二元一次方程,从而求出A,B的值.
解答:

(2)复杂分式方程
例2
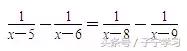
分析:
本题若一次性去分母,最简公分母很复杂,因此,可以等式两边分别通分,观察分子之后,继续往下做.
解答:
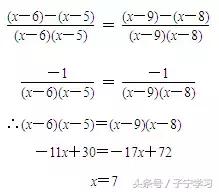

 加载中,请稍侯......
加载中,请稍侯......
精彩评论