「高中数学」三角形四心与向量

掌握四心问题，解决四心类拓展问题需要掌握住四心问题用向量法的证明方法，另外再结合向量专题中常用的向量共线点共线的结论即可。

重心的证明需要确定出动点所在的向量和中线向量共线即可，即存在常数λ

垂心的证明一般利用动点所在的向量乘对边向量为零。

外心的证明是重心和垂心的结合（中垂线）

内心的证明需要证明动点所在的向量和角平分线所在的向量共线，因此若要出现角平分线，则在两腰长不相等的条件下各自取其单位向量即可。

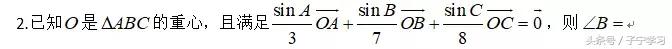
解读：注意重心在向量专题中的一个常用结论：从重心出发到三个顶点的向量之和(若各自存在系数，则系数相等)为零向量。

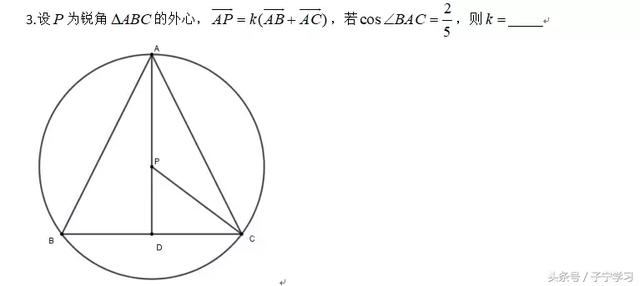
题目重点注意等腰三角形底边上的高线，中线重合。

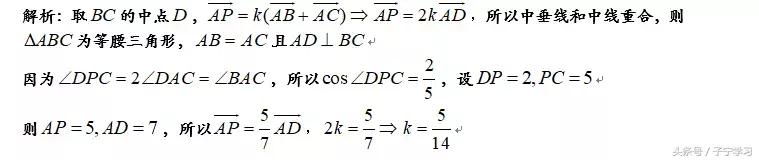
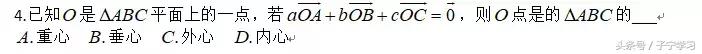
解读：题目也是个结论，需要记下来，判定是什么心，我们需要变形得到共线关系或者向量乘积为0的关系，而且一般也需要从该点到三个顶点的一点的向量和另外两条边长向量的关系，因此该题目很自然想到需要变形，变形之后自然而然也就知道是什么心了。

注意红框中表示两个单位向量相加，之后的向量与角A角平分线的方向一致。

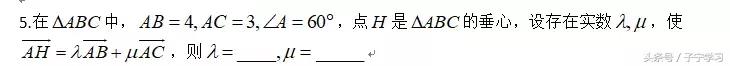
解读：垂心问题很容易想到需要乘对边所在的向量，这样相乘之后会是0，利用两次即可，解法中给出了用三点共线的方法来求解，比乘向量要简单。

解读：注意向量中如果出现两个数之和为1，则一定要想到肯定存在三点共线，这也是题目出题的题眼所在。