八年级数学一次函数的图像和性质（2）

一、知识回顾与总结：

1、一次函数 y = kx + b ( k ≠ 0 ) 的图像是经过点 （0 ， b ) 和 （-b/k , 0 ) 的一条直线；

2、一般地，一次函数 y = kx + b ( k ≠ 0 ) 的性质是：

当 k > 0 时，y 随 x 的增大而增大 ；

当 k < 0 时，y 随 x 的增大而减小 。

此性质反映在图像上是：

当 k > 0 时，图像自左而右是上升的 ；

当 k < 0 时，图像自左而右是下降的 。

二、重点题型剖析与总结：

题型一 直线在平面直角坐标系中的位置

例题1、两直线 y1 = kx + b 和 y2 = bx + k 在同一平面直角坐标系内的位置可能是 （ A）

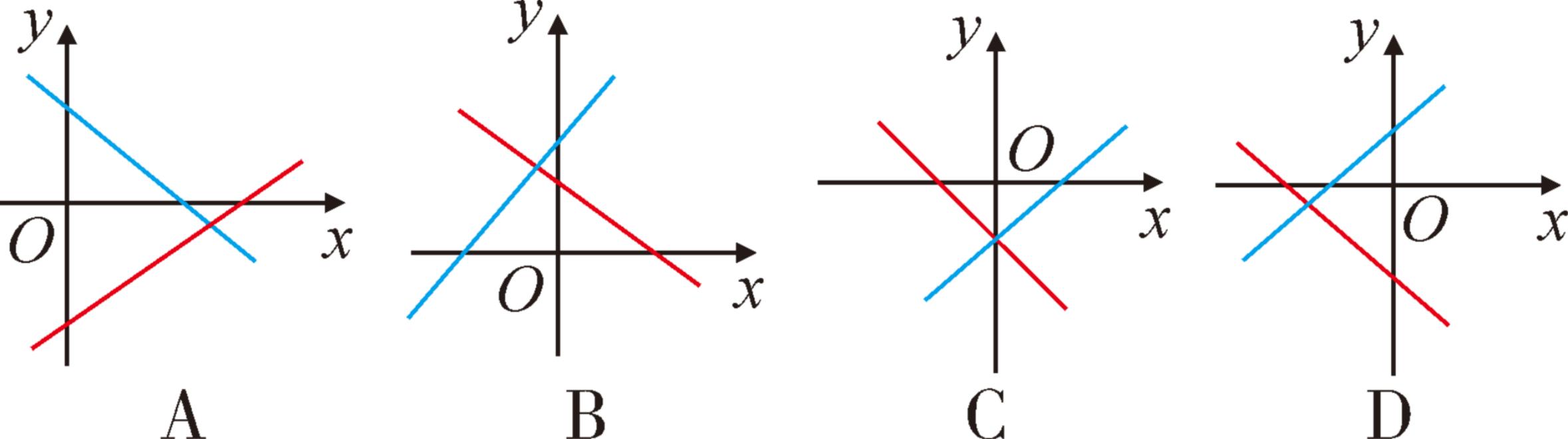
解题思路：

分别确定各选项中，两直线 k，b 对应的取值范围 ，找 k，b 的取值范围相同的即可得到答案。

练习、下列直线大致如图所示的是 （ B ）

题型二 一次函数的图像和性质的综合运用

例题2、已知一次函数 y = ( m - 2 )x - m^2 / 4 + 1 .

(1) 当 m 为何值时 ，函数的图像经过原点；

(2) 当 m 为何值时 ，函数的图像与 y 轴交于点 （0 ，-3 ）；

(3) 当 m 为何值时，函数图像平行于直线 y = 2x 。

题型三 实际问题中的一次函数的图像

例题3、星期天，李小刚同学随爸爸、妈妈回老家探望爷爷、奶奶.爸爸 8：30 骑自行车先走，平均每小时骑行 20 km；李小刚同学和妈妈 9：30 乘公交车后行，公交车平均速度是 40 km/h。爸爸的骑行路线与李小刚同学和妈妈的乘车路线相同，路程均为 40km。

设爸爸骑行时间为x（h）。

（1）请分别写出爸爸的骑行路程 y1（km）、李小刚同学和妈妈的乘车路程 y2（km）与x（h）之间的函数表达式，并注明自变量的取值范围；

（2）请在同一个平面直角坐标系中画出（1）中两个函数的图像；

（3）请解答谁先到达老家。

解题思路：

根据速度乘时间等于路程，可得函数表达式 ；

用描点法，可得函数图像，再根据图像，解答（3）。

题型四 一次函数的图像和图形面积的综合

例题4、在平面直角坐标系中，直线 y = 2/3 x - 2/3 与长方形 ABCO 的边 OC，BC 分别交于点 E，F，已知 OA=3，OC=4，求 △CEF 的面积。

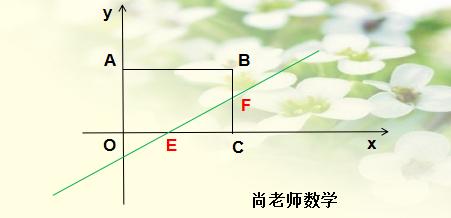
三、知识拓展与提高：

例题5、已知一次函数 y = ax - a + 1 ( a 为常数，且 a ≠ 0 ) .