五六年级数学：求阴影面积七题，三角形长方形正方形圆和扇形综合

cc518学习网精品学习资料总目录

题一

分析解答

方法1.S阴=S△ADE--S△ADF=1/2AD.DC--1/2AD.AF=1/2×8×6--1/2×8×（6--2）=8平方厘米.

方法2.连接BD。∵△AEB和△DEB同底（EB）等高（AB=CD)，∴二者面积相等。再同时减去公共部分△EFB，S阴=S△FDB=1/2FB×AD=1/2×2×8=8平方厘米。

题二

分析解答

紧紧抓住底边共线的共顶点三角形（此底边上的高相等）面积之间的关系解题。

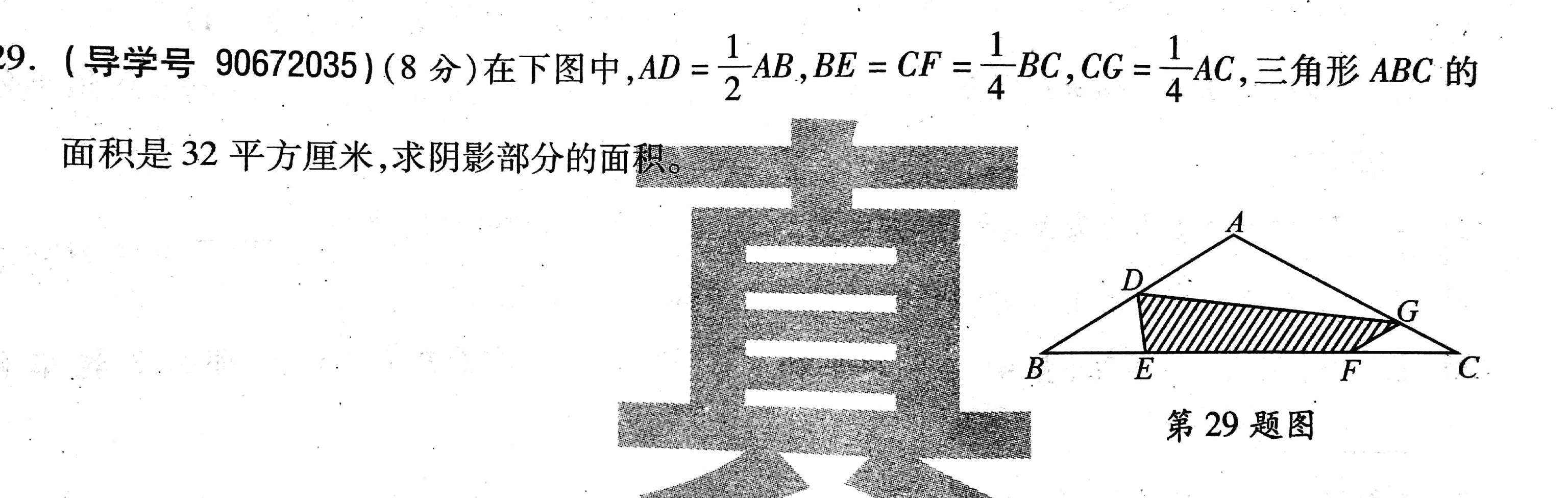
连接AE、AF。∵BE=CF=1/4BC，∴S△ABE=S△AFC=1/4S△ABC=1/4×32=8平方厘米。

在△ABE中，∵AD=1/2AB,∴S△ADE=1/2S△ABE=1/2×8=4平方厘米=S△BDE。

在△AFC中，∵CG=1/4AC，∴S△CGF=1/4S△AFC=1/4×8=2平方厘米。

连接CD，∵CG=1/4AC，∴AG=（1--1/4)AC=3/4AC.

∴S△ADG=3/4S△ADC=3/4×1/2S△ABC=3/8×32=12平方厘米。

∴S阴=32--4--2--12=14平方厘米。

题三

分析解答

既然没有告诉小正方形的边长，说明计算结果应该与此条件无关。不妨设小正方形边长为1（要小于4）。

方法1.分割。连接AE、AC，阴影部分被分割为四块。S△AEF=1/2EF.GF=1/2×1×1=1/2.

S△AEC=1/2EC.AB=1/2×(4-1)×4=6.

S△CEF=1/2EF.EC=1/2×1×(4-1)=3/2.

S弓形=S扇形-S△ABC=1/4π.4²-1/2×4×4=4π-8.

∴S阴影=1/2+6+3/2+4π-8=4×3.14=12.56cm².

方法2.补足。分别延长DC、GF，相交于点M.

S长方形AGMD=4×（4+1）=20.

S左下角空白=S正方形ABCD-S扇形=4×4-1/4π4²=16-4π.

S右上角空白=1/2AG.GF=1/2×(4+1)×1=5/2.

S右下角空白=1/2CM.MF=1/2×1×(4-1)=3/2.

∴S阴影=20-（16-4π）-5/2-3/2=4×3.14=12.56cm².

题四

分析解答

观察图形，可见阴影弓形正好可以移到右边正方形中，这样S阴影=1/2S正方形=1/2×6×6=18cm².

题五

分析解答

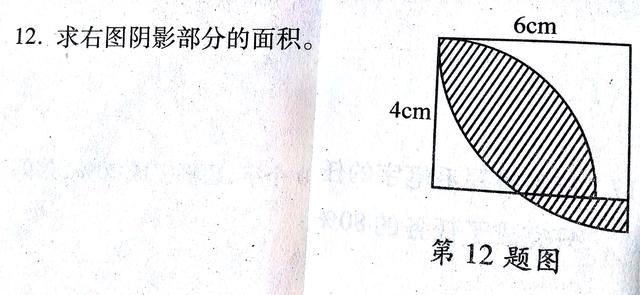
观察图形，阴影部分不规则，但它含在右边以6cm为半径的扇形中，说明要减去右边这个空白部分面积。而这部分面积又可以用长方形面积减去左边以4cm为半径的扇形面积而得，问题可解。

S右空白=S长方形-S小扇形=4×6-1/4π×4²=24-4π.

S阴影=S大扇形-S右空白=1/4π×6²-（24-4π）=13×3.14-24=16.82cm².

题六

分析解答

和长方形、正方形、平行四边形以及梯形中隐含着平行线段的条件不一样，本题明确告诉了DE与AC平行。夹在平行线间的三角形隐含着同高的条件，如果底又相等，这样的三角形面积就相等，从而可以实现图形转移，从不规则图形变为规则图形，方便求面积。

连接OD、OE。∵DE与AC平行，∴S∆ADE=S∆ODE，阴影部分就变成了一个规则的扇形.

∵DE=DO=EO=3cm,∴∆ODE是等边三角形，∠DOE=60º.

于是S阴影=60º/360º×3.14×3²=4.71cm².

题七

分析解答

只介绍最简单的一种方法。连接两个正方形的对角线，则二者平行。所以上下一白一黑两个小直角三角形面积相等。阴影部分就转化为一个扇形，面积为1/4×3.14×4²=12.56cm².

总结:小学数学中求阴影部分面积一类的题目，变化很多，综合性强。只要同学们扎实基础，善于观察，念好“割”、“补”、“移”三字经，定会迎刃而解。