中考数学压轴题进阶训练8解决线段“PA+k×PB”型问题

“PA＋k·PB”型的最值问题，当k＝1时通常为轴对称之最短路径问题，而当k＞0时，若以常规的轴对称的方式解决，则无法进行，因此必须转换思路．

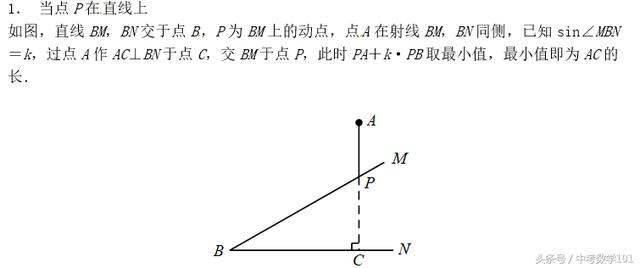
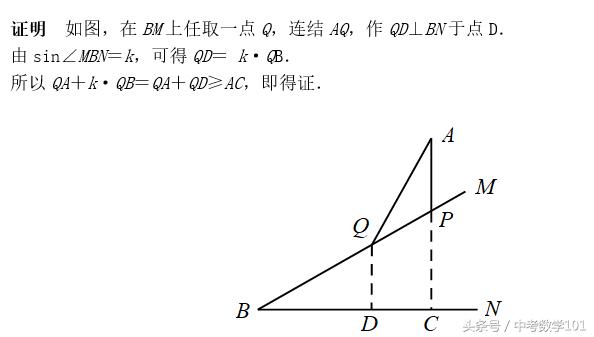
1． 当点P在直线上如图，直线BM，BN交于点B，P为BM上的动点，点A在射线BM，BN同侧，已知sin∠MBN＝k，过点A作AC⊥BN于点C，交BM于点P，此时PA＋k·PB取最小值，最小值即为AC的长．

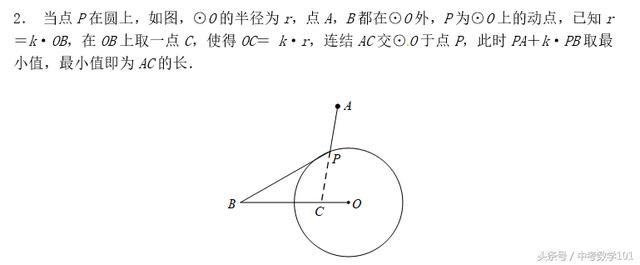
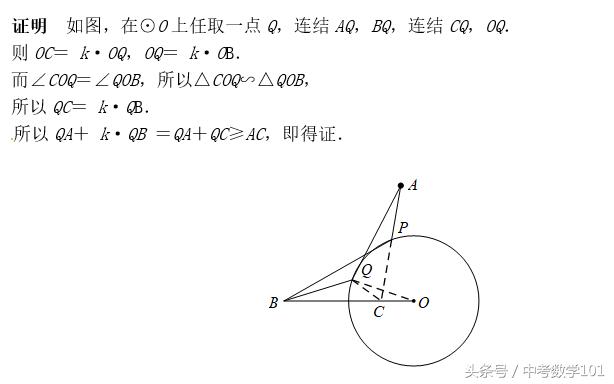
2． 当点P在圆上，如图，⊙O的半径为r，点A，B都在⊙O外，P为⊙O上的动点，已知r＝k·OB，在OB上取一点C，使得OC＝ k·r，连结AC交⊙O于点P，此时PA＋k·PB取最小值，最小值即为AC的长．

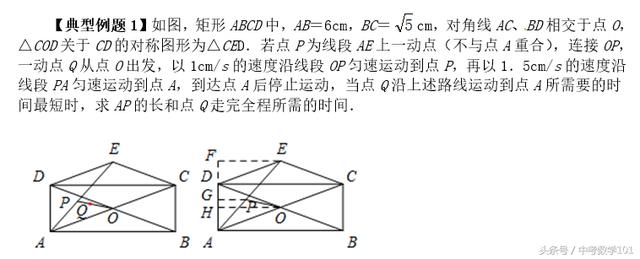
【典型例题1】如图，矩形ABCD中，AB＝6cm，BC＝根号5cm，对角线AC、BD相交于点O，△COD关于CD的对称图形为△CED．若点P为线段AE上一动点（不与点A重合），连接OP，一动点Q从点O出发，以1cm/s的速度沿线段OP匀速运动到点P，再以1．5cm/s的速度沿线段PA匀速运动到点A，到达点A后停止运动，当点Q沿上述路线运动到点A所需要的时间最短时，求AP的长和点Q走完全程所需的时间．

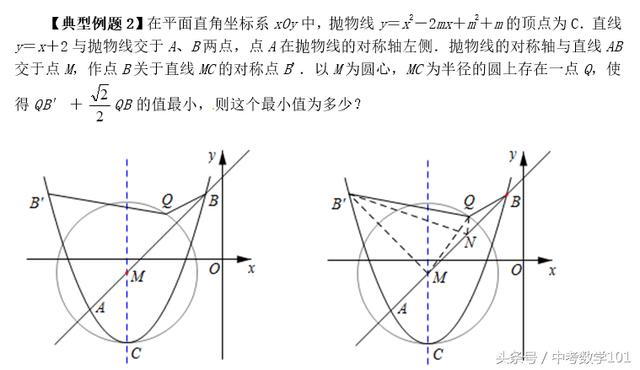
【典型例题2】在平面直角坐标系xOy中，抛物线y＝x²－2mx＋m²＋m的顶点为C．直线y＝x＋2与抛物线交于A、B两点，点A在抛物线的对称轴左侧．抛物线的对称轴与直线AB交于点M，作点B关于直线MC的对称点B'．以M为圆心，MC为半径的圆上存在一点Q，使得QB′＋QB的值最小，则这个最小值为多少？