1题4解求动点P点坐标，全面讲解二次函数中，三角形面积最值问题

二次函数，是中考的一个重点，也是一个难点。特别是压轴大题，代数几何综合题型，更是考试常见。但是，很多同学觉得这类题型实在太难，望而生畏。

比如二次函数图像中，抛物线先上是否存点动点P，使得三角形面积最大，然后求出动点P此时的坐标。这就是最经典最常见的二次函数图像面积最值问题。

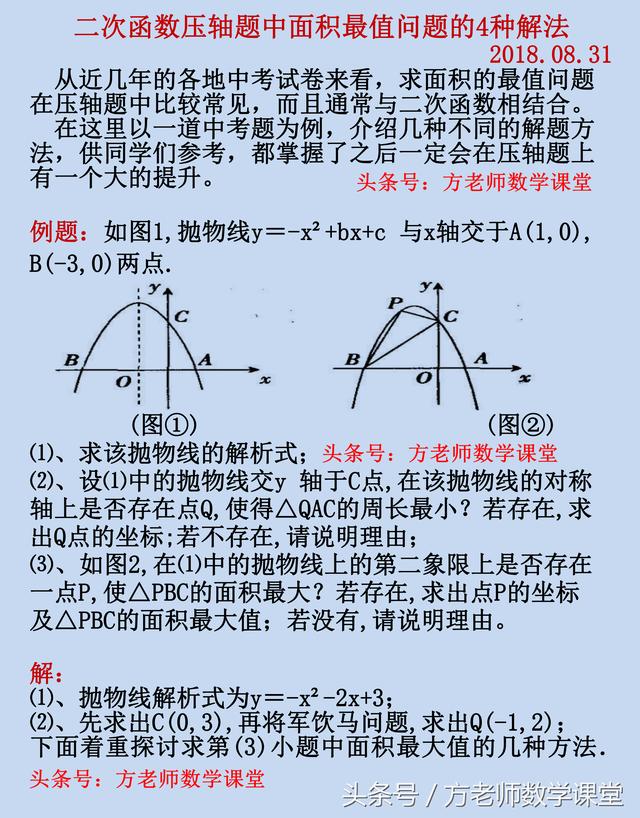
今天，通过一道中考真题，用四种不同的方法来一起探讨这一类题型。希望同学们认真体会，理解透彻，举一反三。

解法一，割补法。就是把通过图形割和补的方式，把三角形的面积求法表达出来。这个方法，最简单最常用。

解法一，方法1，设动点P的坐标，△PBC的面积等于△PBE面积加梯形的面积，再减去三角形BOC的面积。

把三角形PBC的面积表达出来，得到一个二次函数的顶点式。即可求出面积最大值。

解法一，方法2。连接PO，三角形PBC的面积等于三角形BOP面积加三角形COP的面积，再减去三角形BOC的面积。

和方法1一样，最后得到一个二次函数的顶点式，即可求出三角形面积的最大值。

解法二、铅垂定理法。上面这个图片，就是铅垂定理的基本知识点。

铅垂定理的求法公式就是，三角形的面积等于水平宽度与铅垂高度乘积的一半。

任何一个三角形，都可以用这个方法来求面积。在直角坐标系中，只要求出一个三角形水平宽度，和铅垂高度，那么这个三角形的面积就出来了。

这个题目，作PE⊥x轴交BC于F，则水平宽度就是OB的长度，铅垂高度就是PF的长度。

后面的就是直接套用铅垂定理的公式，经过化简，得出二次函数的顶点式，即可求出三角形面积最大值。

请看详细解题过程，铅垂定理真的很重要。很多题型中，铅垂定理求面积更简单。

解法三，切线法。切线法，就是过点P做BC的平行线，当这个平行线与二次函数的图像只有一个交点时，则BC边上的高就是最大值。

底一定，高最大，当然面积最大。请看详细解题过程。有问题，欢迎评论区留言。

解法四、三角函数法。这个方法看起来好像很难，其实也很简单。详细请看解题过程。

同学们也可以通过这个方法，来练习和巩固一下三角函数知识和相关题型。

总之，从以上四种解法的基本思路，都是过点P作辅助线，设P的坐标。然后把相关的线段用含未知数的代数式表达出来，根据面积求法公式，得到一个二次函数的顶点式，即可得到面积的最大值，和P点的坐标。