「初中数学」全局思维和动态思维

我们以实例说明如何在解题运用和训练全局思维和动态思维。

例.如图，已知正方形ABCD和正方形CEFG，连接BG、DE、AF，分别取它们的中点P、M、N，求证：四边形PCMN是正方形。

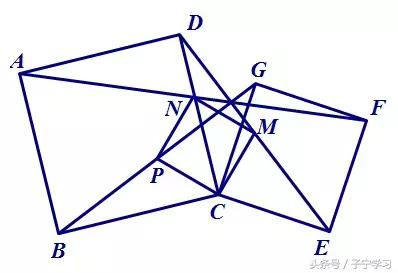
审题与思考就是把信息结构化，把混沌信息转化为有序结构。

引导性问题：

（1）怎么看两个正方形的关系？

[其中一个可以看成另一个绕公共顶点旋转任意角度并缩放所得。]

脑补图是这样滴：

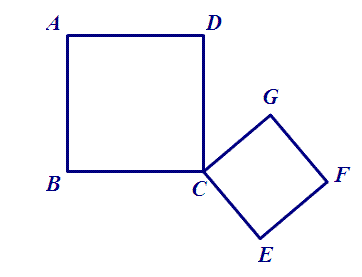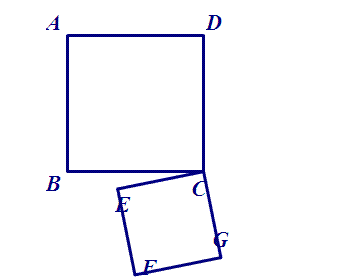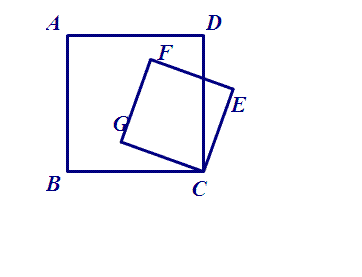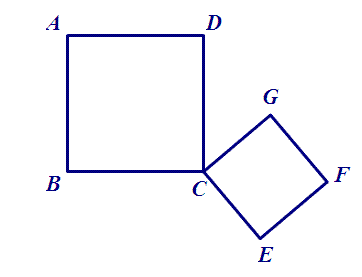
（2）图中有三角形关系吗？

[正方形可以分解成等腰直角三角形，得另一对全等三角形，并且是旋转90度。手拉手模型：ΔBCG旋转90度得ΔDCE。]

脑补图如下：

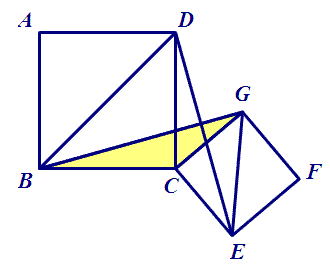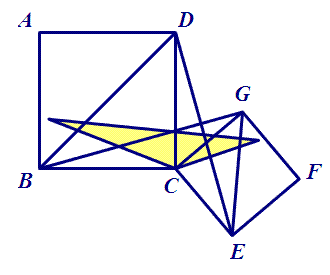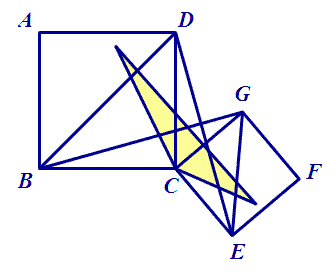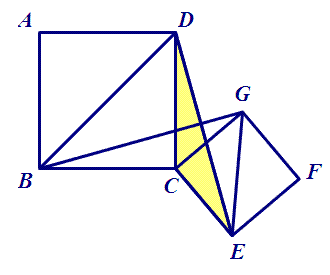
（3）CP与CM是什么关系？由此，能得出CP与CM的关系吗？

[CP、CM分别是ΔBCG、ΔDCE对应边上的中线，当然也是和三角形一样旋转90度的关系，能证CP与CM也是相等且垂直。]

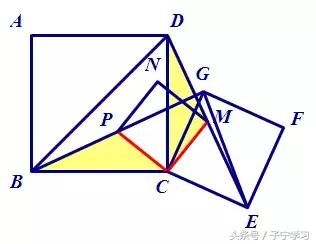
（4）已经成功一半了，再看AF在整个图形中是什么角色？

[AF、BG是共顶点的一对等腰直角三角形的对应点连线，由一转成双知ΔBCG与ΔACF也相似，且是旋转45度并放大1:√2关系。]

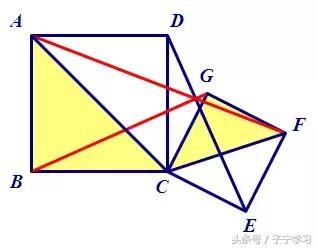
（5）继续前进，CP、CN又是什么角色？

[CP、CN是相似三角形对应边上的中线，可得CP:CN=1:√2，且∠PCN=45°。]

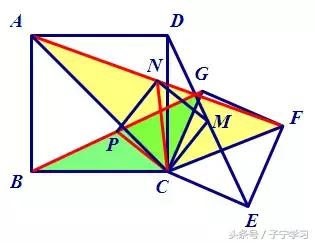
（6）到此已得ΔPCM、ΔPCN都是等腰直角三角形，问题得证。

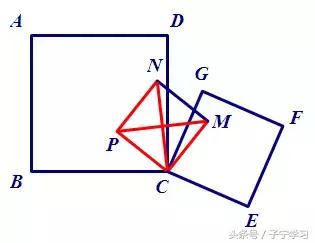
全局视角能看到局部元素在整体中扮演的不同角色，动态视角能看到元素之间的变换生成关系。