数列隔项(奇偶项)符合一般递推规律的一类问题是数列中一种常见题型，这类问题学生往往对奇偶分类搞混淆，那么本文就针对这一类问题给出解题策略与方法总结.

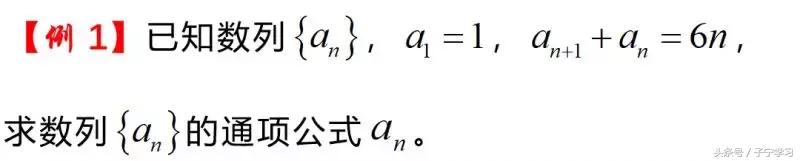
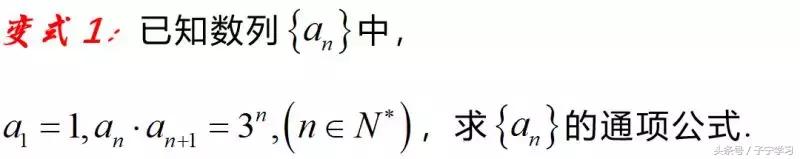
「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


【分析】第（Ⅱ）为探索题.对于探索题的解法，通常我们先假设存在，用特殊项，比如利用前3项成等差，求出参数的值（这个过程利用的是条件的必要性）；然后再验证该参数的值的确使得该数列为等差数列（这个过程是证明条件的充分性）.

「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


【总结】本题采用的特殊到一般的数学思想，本题在验证an为等差数列时，是通过递推关系分别求出奇数项与偶数项的通项公式，最终可求出an的通项公式，进而可证明为等差数列.

「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略


「高中数学」数列隔项递推求通项的解题策略

「高中数学」数列隔项递推求通项的解题策略