辅助线不会添？添了又不满足结论？基本图形分析法教你如何添线

今天的这道例题相对之前的全等例题稍微有些难度，本题的关键就体现在了辅助线的添加，要如何根据求证结果去添加正确的辅助线。基本图形分析法给出此题的两种辅助线添加方法，来满足求证结果在直角三角形中，并根据轴对称型全等三角形性质得到对应的等价条件，完成整个分析过程。来看看你是不是也想到了这两种方法吧~

例18 如图5-48，已知：△ABC中，∠ACB=90°，AC=BC，D、E是AB上的两点 ，∠DCE=45°，求证：DE²=AD²+BE²。

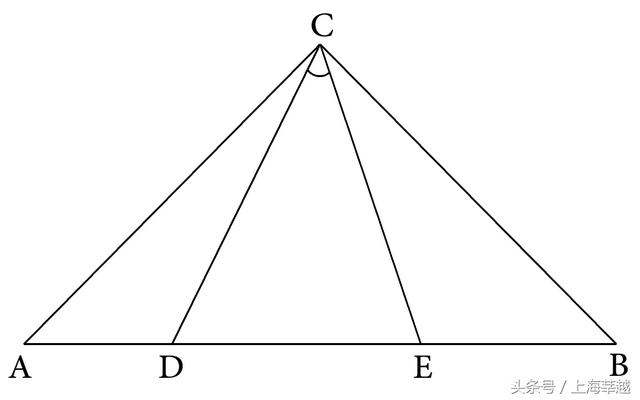
图5-48

分析 （1） ：本题条件中出现了∠DCE=45°，且∠ACB=90°，所以∠DCA+∠ECB=90°-45°=45°，这是一个两个角之和的问题，所以可根据两角和的定义，将∠DCA和∠ECB这两个角拼起来，也就是以C为顶点，以CA为一边，在△ABC的外面，作∠ACF=∠ECB，这样就可得∠DCF=45°，∠DCF=∠DCE。而这两个角相等的关系一出现，就出现了这两个相等的角是关于CD成轴对称的，从而就可以添加轴对称型全等三角形进行证明，于是在所作的∠DCF的边CF上，截取CF=CE，并联结DF（如图5-49），就可由CF=CE，∠DCF=∠DCE=45°和DC=DC，证得△DCF≌△DCE，DE=DF。

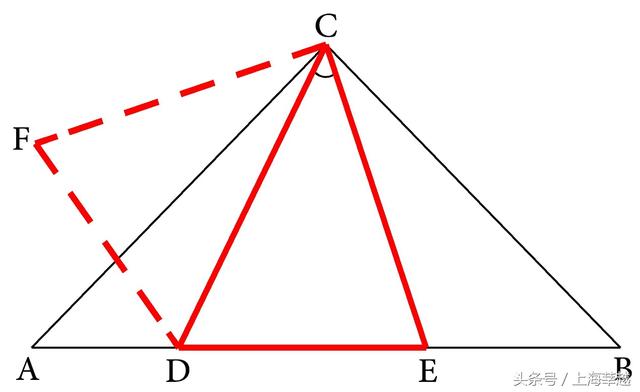
图5-49

由我们所作的CF=CE和∠ECF=45°+45°=90°，可知CF、CE可组成一个等腰直角三角形，而已知△ABC也是等腰直角三角形，且这两个等腰直角三角形有公共的直角顶点C，所以必定出现一对旋转型全等三角形。找这对全等三角形的方法是将由公共顶点C发出的四条线段，即CF、CA、CE、CB两两组成全等三角形，于是联结AF（如图5-50），那么在△ACF和△BCE中，由AC=BC，∠ACF=∠BCE和CF=CE，就可得△ACF≌△BCE，那么AF=BE，∠CAF=∠CBE=45°，进一步就可得∠FAB=45°+45°=90°，而在Rt△FDA中，应用勾股定理就有DF²=AD²+AF²，而DF=DE，AF=BE，所以分析可以完成。

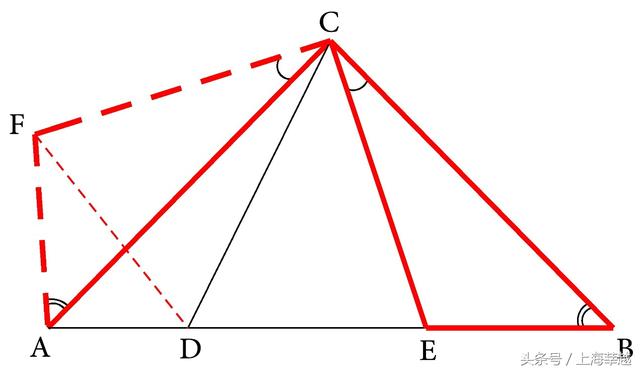
图5-50

分析 （2） ：本题条件中出现了∠DCE=45°，∠ACB=90°，所以就有∠DCA+∠ECB=45°=∠DCE，那么根据角的和的定义，就可以在∠DCE内作∠DCF=∠DCA，然后可得∠ECF=∠ECB。

在作出了∠DCF=∠DCA后，就出现了这两个相等的角是关于DC成轴对称的（如图5-51），从而就可添加轴对称型全等三角形进行证明。

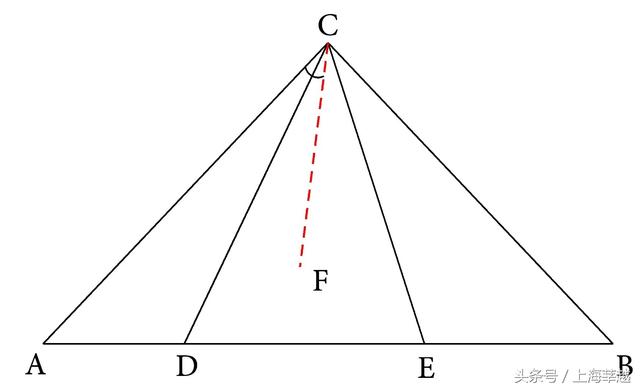
图5-51

由于图形中已经出现了对称轴CD，所以添加的方法就是将△ACD沿对称轴翻折过去，这时因∠DCA=∠DCF，所以CA就会沿CF落下，于是就可以在射线CF上截取CF=CA，联结DF后（如图5-52），就可得△ACD≌△FCD，∠F=∠A=45°和DF=DA。根据同样的道理，在联结EF后（如图5-53），由CF=CA=CB，∠FCE=∠BCE和CE=CE，又可证明△FCE和△BCE也是一对轴对称型全等三角形，所以FE=BE，∠EFC=∠B=45°，进一步就可得∠DFE=45°+45°=90°，这样在直角△DEF中，就可应用勾股定理得DE²=DF²+EF²，从而也可完成分析。

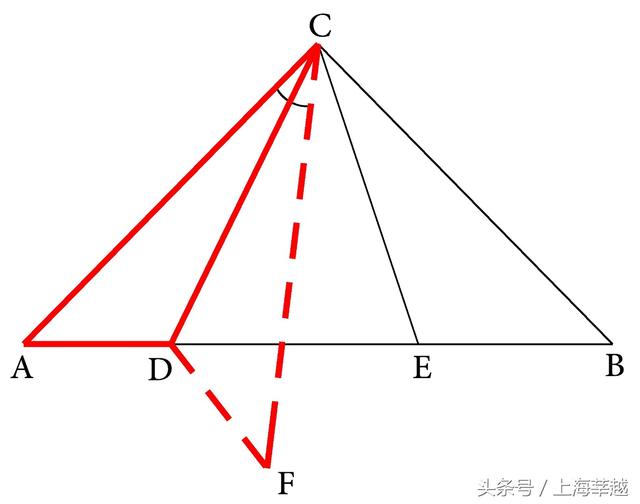
图5-52

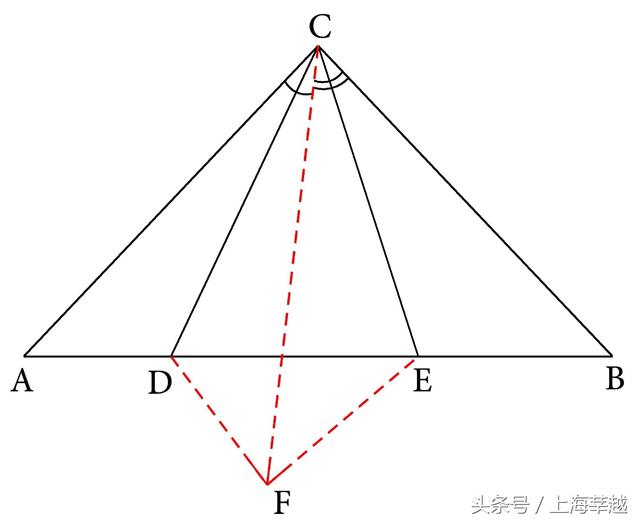
图5-53