压轴题放送：四个因动点产生的面积问题，函数图像最受青睐

第一题给出了一个正方形ABCD的几何图形，然后设置了一个动点P在正方形 ABCD的边上运动，设置一个动点Q在x轴上运动，从而形成一个一个动态的三角形OPQ。求函数解析式、求点的坐标，求动态三角形的面积最大等等一系列复杂的问题就在这样的基础上形成了。

第二道题，与第一题类似，但是给出的是一个等腰梯形，给出一些几何关系和边角情况，看似简单，但是问题可是有一定的水平：特别是第二问，你需要先拿下这个还没在图上成型的虚拟抛物线；然后才有第三问动点P在抛物线上运动时的一些规律情况！当然，题干上还有tan这样的正切知识点，回顾正玄余玄之类的哦。

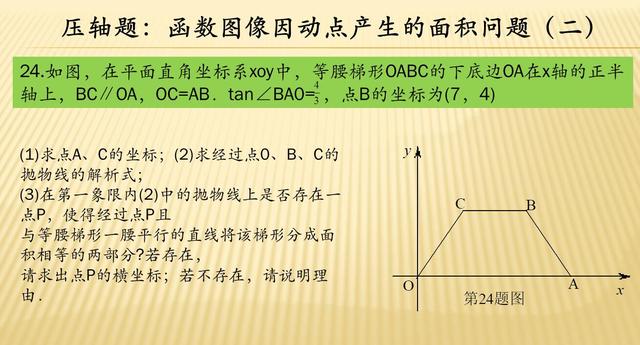
第三题同样给出一个矩形作为基础图形，然后告诉你一些坐标和一根已知位置的直线，也就是说，看似整个题干已经把关系全部挑明了，然后问题就有点懵了：两个小文都是面积关系，而且第二问球的一个重叠部分的面积，你需要先搞清楚谁和谁重叠，然后重叠出来的是什么东西，他们之间的几何关系和解析式怎样表达，内容非常丰富。

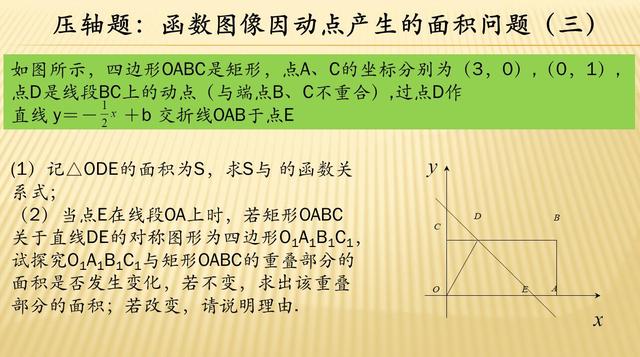
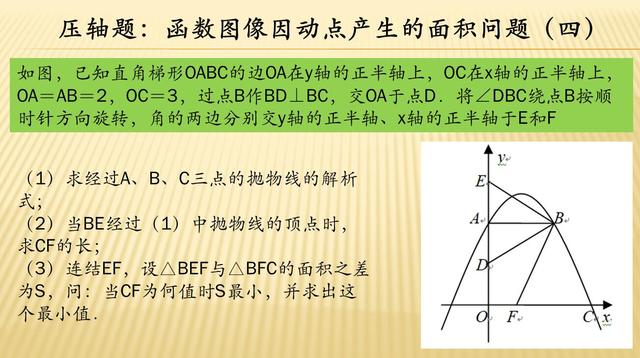
最后一题，同样给出一个直角梯形作为底图，然后再添上一根抛物线、一个垂直关系，一个旋转的角度，然后形成了这几题中最复杂的一个图形，特别注意的是，这题的1、2、3问是循序渐进的并不突兀，一股脑专注解下去，尝试抽丝剥茧吧，算是题目给出的一点小提示了。