「初中数学」一类倒数和模型的探究

本文拟以一类倒数和模型为研究背景，从代数说理和几何推理两方面加以论证，探究以题会类，以达说一题，通一片之效.

先从本区域结束不久的六校联考压轴题说起，其来源是2017年广西南宁市、北海市、钦州市、防城港市中考数学压轴题.

三、解后反思

大数学家笛卡尔经典佳句：“我思故我在！”

反思是最可贵的学习品质，也是提升解题技能的重要捷径！不反思，不解题！只有反思，才可以将所学化为己有，并逐步内化为能力，长此以往，日积月累，终有所成！

2.1 等腰处理

本题第（2）问是一道等腰三角形存在性问题，既可以采取代数法盲解盲算，也可以通过作图的方式，即两圆一线法，找到所有需要的点P，然后逐个击破，口算与计算并用，方为上策，这本身也是几何法与代数法的完美演绎.

在某些等腰三角形存在性问题中，所谓“两圆”得到的交点坐标有时可以口算完成，而“一线”得到的交点坐标往往需要一定的计算求得，这时候代数法就粉墨登场了.

需要提醒的是，本题中的点P2应舍去，原因是A、D、P2三点共线，此时构不成三角形.可见计算后检验的重要性，这也是考场上很多学生的易错之处.

但特殊值（点）法并不适合于书写解答题，这也是部分考生的易错之处.

再看上述各种解法，代数法给人以脚踏实地、步步为营之感：其中方法1基于因果关系分析，先设出直线l的解析式，求出相应的交点坐标.特别地，在表示AM的长度时，巧妙抓住60°角，简化了运算；方法2则抓住特殊角，巧设边长，结合相似，表示出相应的线段长，可谓“牵一发而动全身”.相比于方法1，此法更显简便，正是因为结合了一定的几何元素，如特殊角、相似等，当然，方法1也可以先巧设边长.

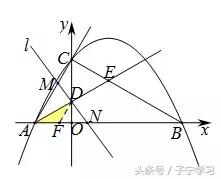
几何法给人以身轻如燕、浑然天成之感：其中方法3利用角平分线，巧作平行线，构造等腰三角形，再结合一步相似即可搞定，这也是笔者最推崇的解法，它能体现出问题的本质，即由角平分线引起的倒数和定值.此外，如右图所示，作DF∥AM交AN于点F，同理可证；

方法4则是见角平分线，作双垂，得相等，然后结合面积法，轻松获解，这也是角平分线常见的处理策略.

由此可见，上述几个面积公式蛮实用，建议熟记并理清其来龙去脉，解答题中若有需要，稍加论证即可.

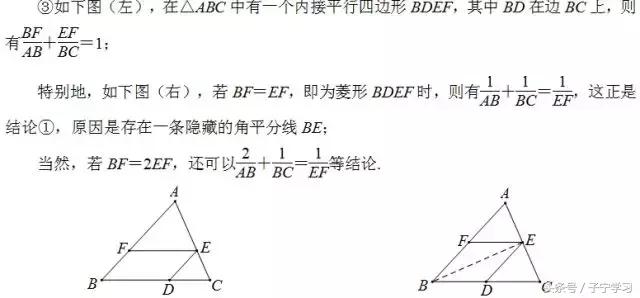
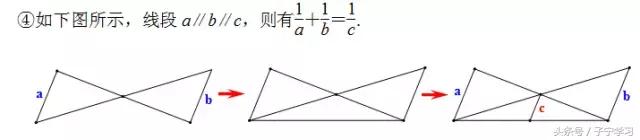
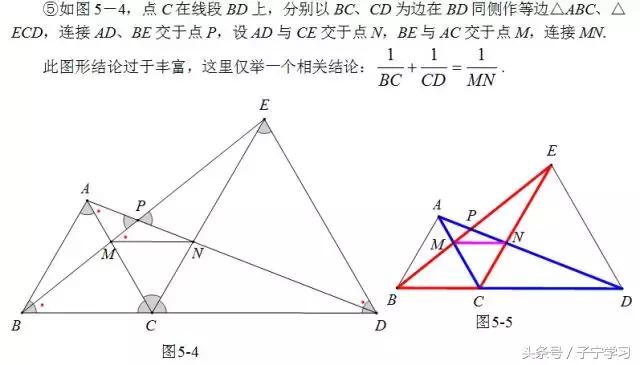
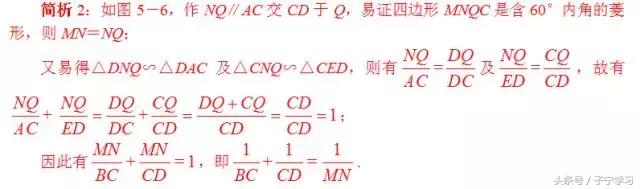
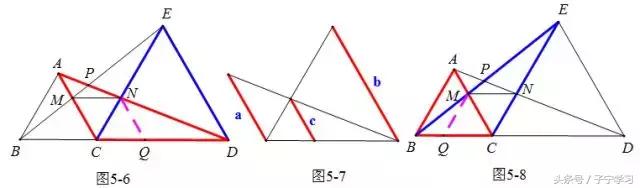
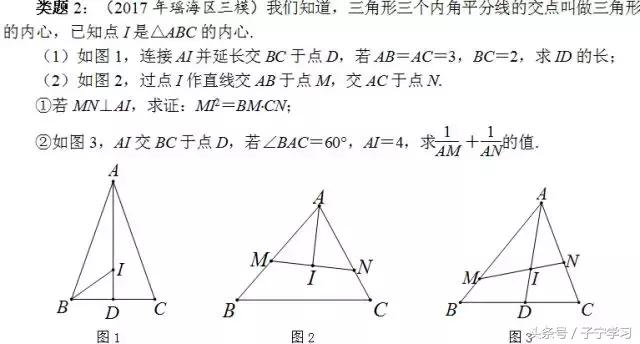
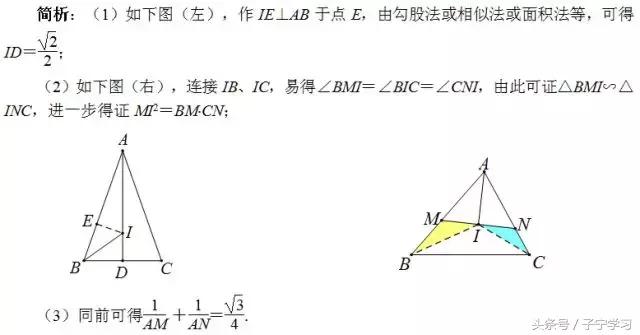
反思：这是一个有趣的图形，内心加垂直，竟然出现了“一线三等角”结构，还是一个中点型“一线三等角”，趣哉！

题以类聚，以题会类，类比探究，其乐无穷.通过本文对于一类因角平分线等引起的倒数和定值问题，从代数说理与几何推理两方面加以论证，相信大家对于此类问题的通解通法有了一定的收获，则此文价值足矣！