平面向量是高中数学知识体系的重要组成部分,由于它具有代数形式和几何形式的“双重身份”,融思想性和工具性于一体,可以沟通代数与几何的许多分支并使之建立起多元联系,因而成为高考命题的热点,对于很多平面向量问题,通过巧妙建立平面直角坐标系,将试题中所有的向量转化为坐标形式,利用向量的坐标使向量运算完全代数化,实现了形向数的转化,这种向量坐标化的做法,可以极大地降低思维难度,成为解决众多向量问题的标准解法,正所谓“向量坐标化,一招定天下”,下面结合具体例子谈谈这类问题的破解策略.
典型题组1 有现成坐标或正交基底,直接坐标化
例题精讲

点评
本题主要考查了平面向量的数量积、平面向量的模等基础知识,意在考查学生的转化与化归能力、数形结合能力和运算求解能力,利用垂直条件建立坐标系、理解单位向量的含义厦其运算是解题的关键所在.
典型题组2 根据图形建立坐标系,使得向量坐标化
例题精讲
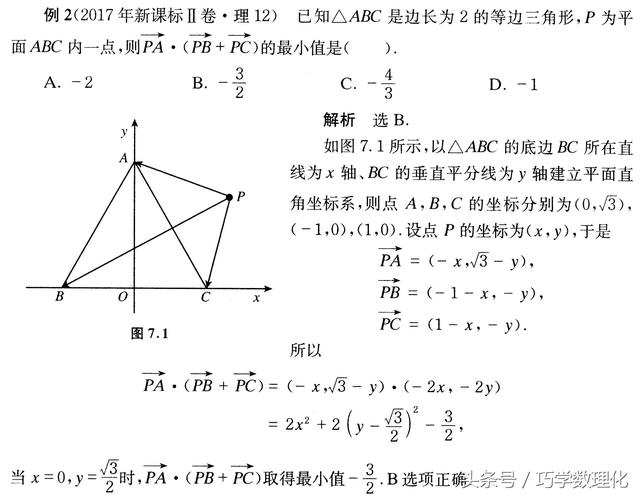
点评
本题以正三角彤为栽体,动点P导致动向量PA、PB、PC。自然想到建立坐标系,将向量关系坐标化,得到数量积的函数表达式,从而确定其最小值,对于平面图形中的向量问题,通过坐标系搭桥,将向量的几何运算转化为代数运算,是一种很好的解题途径.
牛刀小试

参考答案:


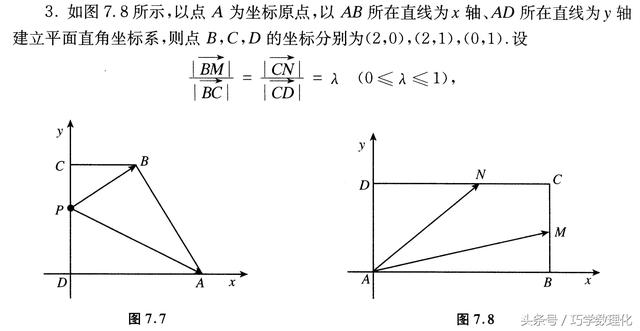
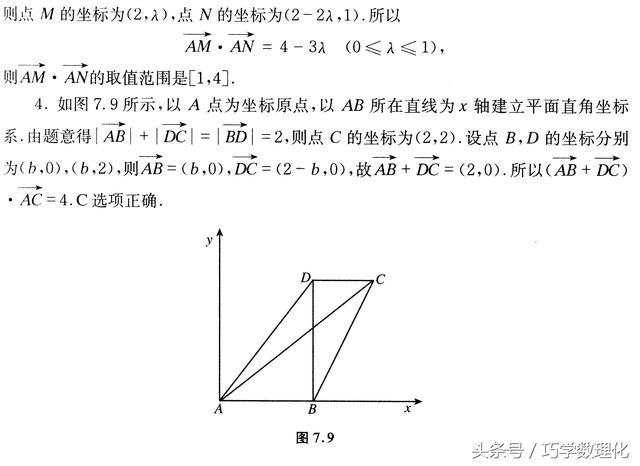

 加载中,请稍侯......
加载中,请稍侯......
精彩评论