中考数学压轴题进阶训练11轴对称与方程思想

成轴对称的两个图形全等；如果两个图形关于某条直线对称，那么对成轴是任何一对对应点所连线段的垂直平分线。通常所说的翻折实质上就是轴对称变换．图形沿着某条直线翻折，这条直线即为对称轴，利用轴对称的性质，再借助方程的知识就能很快解决问题。

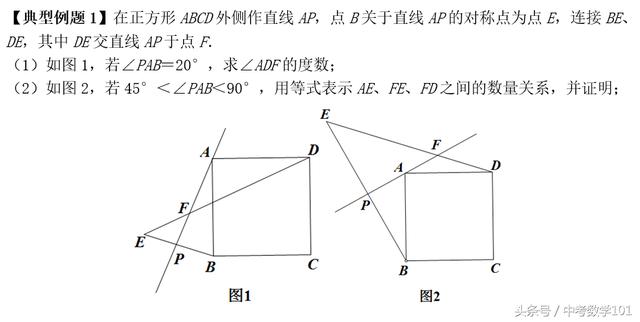
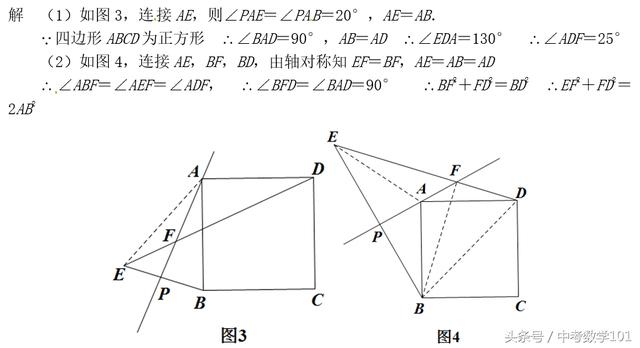
【典型例题1】在正方形ABCD外侧作直线AP，点B关于直线AP的对称点为点E，连接BE、DE，其中DE交直线AP于点F．

（1）如图1，若∠PAB＝20°，求∠ADF的度数；

如图2，若45°＜∠PAB＜90°，用等式表示AE、FE、FD之间的数量关系，并证明；

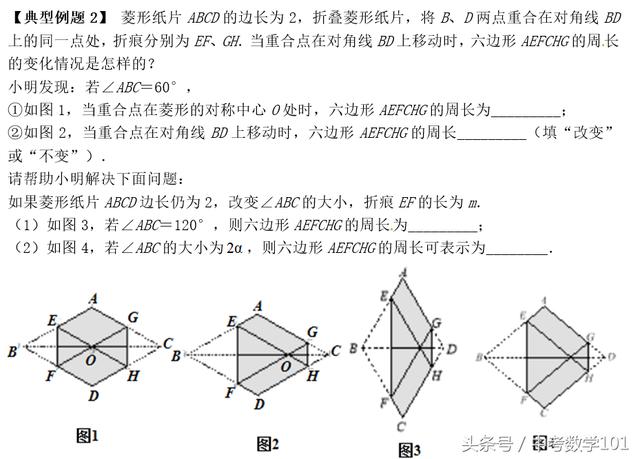
【典型例题2】 菱形纸片ABCD的边长为2，折叠菱形纸片，将B、D两点重合在对角线BD上的同一点处，折痕分别为EF、GH．当重合点在对角线BD上移动时，六边形AEFCHG的周长的变化情况是怎样的？

小明发现：若∠ABC＝60°，

①如图1，当重合点在菱形的对称中心O处时，六边形AEFCHG的周长为_________；

②如图2，当重合点在对角线BD上移动时，六边形AEFCHG的周长_________（填“改变”或“不变”）．

请帮助小明解决下面问题：

如果菱形纸片ABCD边长仍为2，改变∠ABC的大小，折痕EF的长为m．

（1）如图3，若∠ABC＝120°，则六边形AEFCHG的周长为_________；

（2）如图4，若∠ABC的大小为，则六边形AEFCHG的周长可表示为________．

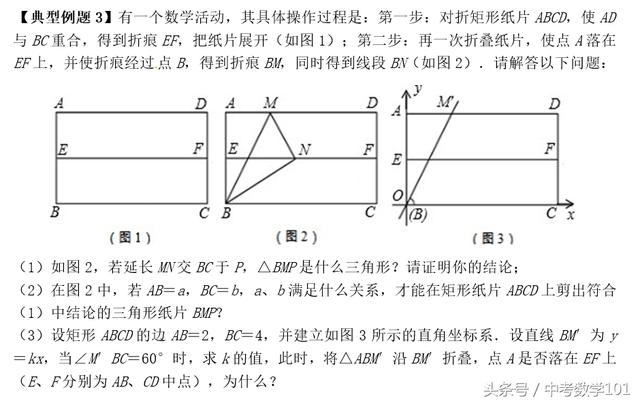
【典型例题3】有一个数学活动，其具体操作过程是：第一步：对折矩形纸片ABCD，使AD与BC重合，得到折痕EF，把纸片展开（如图1）；第二步：再一次折叠纸片，使点A落在EF上，并使折痕经过点B，得到折痕BM，同时得到线段BN（如图2），请解答以下问题：

如图2，若延长MN交BC于P，△BMP是什么三角形？请证明你的结论；

（2）在图2中，若AB＝a，BC＝b，a、b满足什么关系，才能在矩形纸片ABCD上剪出符合（1）中结论的三角形纸片BMP？

（3）设矩形ABCD的边AB＝2，BC＝4，并建立如图3所示的直角坐标系．设直线BM′为y＝kx，当∠M′BC＝60°时，求k的值，此时，将△ABM′沿BM′折叠，点A是否落在EF上（E、F分别为AB、CD中点），为什么？