与三角形有关的动态综合问题

三角形作为几何王国当中最基本、最重要内容之一，在整个中学数学内容中，占据很重要的位置。我们认真研究和分析很多几何综合问题，发现这些大题，都能拆分成若干个三角形，如等腰三角形、等边三角形、直角三角形等，学会运用这些特殊三角形的性质去分析问题和解决问题。

举个简单的例子，任何一个与四边形有关的问题，我们只要做出对角线等，就可以构造一些三角形，此时综合运用它的性质和定理，就能顺利解决问题。

中考除了考查大家掌握必要的知识内容和方法技巧之外，更加考查考生运用知识分析问题和解决问题的能力。因此，在中考数学试卷当中，除了基础题之外，还有一些与三角形有关的综合应用问题，像三角形有关的动态综合问题。

典型例题分析1：

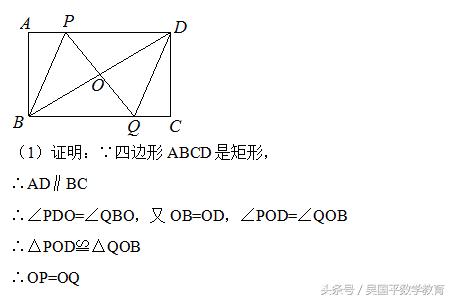
如图，矩形ABCD中，点P是线段AD上一动点，O为BD的中点，PO的延长线交BC于Q．

（1）求证：OP=OQ；

（2）若AD=8厘米，AB=6厘米，P从点A出发，以1厘米/秒的速度向D运动（不与D重合）．设点P运动时间为t秒，请用t表示PD的长；并求t为何值时，四边形PBQD是菱形．

考点分析：

相似三角形的判定与性质；全等三角形的判定与性质；勾股定理；菱形的性质；矩形的性质；证明题；动点型。

题干分析：

（1）本题需先根据四边形ABCD是矩形，得出AD∥BC，∠PDO=∠QBO，再根据O为BD的中点得出△POD≌△QOB，即可证出OP=OQ．

（2）本题需先根据已知条件得出∠A的度数，再根据AD=8厘米，AB=6厘米，得出BD和OD的长，再根据四边形PBQD是菱形时，证出△ODP∽△ADB，即可求出t的值，判断出四边形PBQD是菱形。

解题反思：

本题主要考查了矩形的性质，在解题时要注意与全等三角形、矩形的知识点结合起来是解本题的关键。

这道动点问题难度不大，只要考生掌握好相似三角形的判定与性质、全等三角形的判定与性质等，就能正确解决问题。

我们都知道，动点问题之所以会难，主要在于它能把很多知识内容结合在一起，形成不同类型的动点综合问题，如函数动点综合问题、代数动点综合问题、函数与几何动点综合问题、几何动点综合问题等，而几何动点综合问题细分的话，又可以分出四边形动点综合问题、三角形动点综合问题、与圆相关的动点综合问题等。

典型例题分析2：

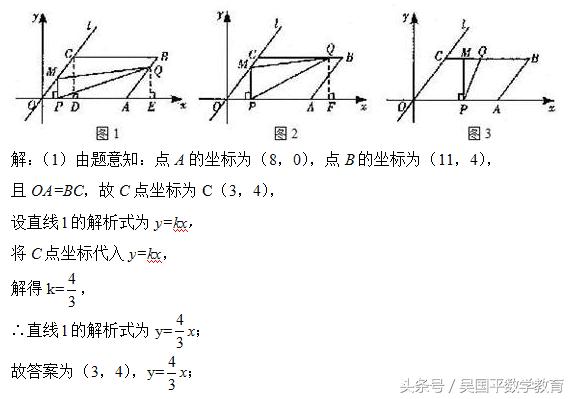
如图，在平面直角坐标系中．四边形OABC是平行四边形．直线l经过O、C两点．点A的坐标为（8，o），点B的坐标为（11.4），动点P在线段OA上从点O出发以每秒1个单位的速度向点A运动，同时动点Q从点A出发以每秒2个单位的速度沿A→B→C的方向向点C运动，过点P作PM垂直于x轴，与折线O一C﹣B相交于点M．当P、Q两点中有一点到达终点时，另一点也随之停止运动，设点P、Q运动的时间为t秒（t＞0）．△MPQ的面积为S．

（1）点C的坐标为 ，直线l的解析式为 ．

（2）试求点Q与点M相遇前S与t的函数关系式，并写出相应的t的取值范围．

（3）试求题（2）中当t为何值时，S的值最大，并求出S的最大值．

（4）随着P、Q两点的运动，当点M在线段CB上运动时，设PM的延长线与直线l相交于点N．试探究：当t为何值时，△QMN为等腰三角形？请直接写出t的值．

考点分析：

二次函数综合题；代数几何综合题；数形结合；分类讨论。

题干分析：

（1）由平行四边形的性质和点A、B的坐标便可求出C点坐标，将C点坐标代入正比例函数即可求得直线l的解析式；

（2）根据题意，得OP=t，AQ=2t，根据t的取值范围不同分三种情况分别进行讨论，得到三种S关于t的函数，解题时注意t的取值范围；

（3）分别根据三种函数解析式求出当t为何值时，S最大，然后比较三个最大值，可知当当t=8/3时，S有最大值，最大值为128/9；

（4）根据题意并细心观察图象可知；当t=60/13时，△QMN为等腰三角形．

解题反思：

本题是二次函数的综合题，其中涉及的到的知识点有抛物线最大值的求法和动点问题等知识点，是各地中考的热点和难点，解题时注意数形结合和分类讨论等数学思想的运用，同学们要加强训练，属于中档题．

与三角形有关的动点问题，主要抓住三角形里的一些不确定因素，如等腰三角形、相似三角形等，需要对边与边之间的关系进行分类讨论。同时，在解决问题过程中，或许还要添加辅助线，这个也是让很多考生头痛的地方。