中考数学复习：射影定理所涉基本图形，弦切角概念，垂径定理

知识科普

射影定理，由古希腊著名数学家、《几何原本》作者欧几里得提出，所以又称“欧几里德定理”，指在直角三角形中，斜边上的高是两条直角边在斜边射影的比例中项，每一条直角边又是这条直角边在斜边上的射影和斜边的比例中项。射影定理是数学图形计算的重要定理。

什么又是比例中项呢？如果a、b、c三个量成连比例，即a:b=b:c，那么b就叫做a和c的比例中项。比例中项是相对于内项相等的比例而言的。数字的比例中项与几何的不一样,可以是正数，也可以是负数。

顺便说开去，平常所说的“黄金分割”原理，就是把一条线段分割成两部分， 使其中较长线段的长是整条线段的长与另一较短线段的长的比例中项。其比值约为0.618。这个比例被公认为是最能引起美感的比例，在绘画、雕塑等领域里有广泛的应用。

射影定理所涉基本图形如下:

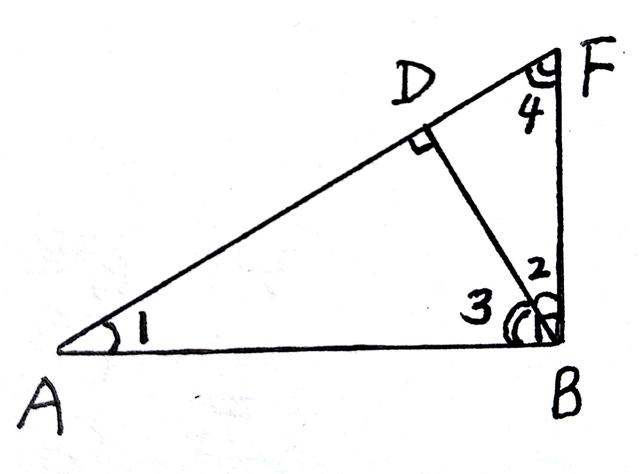
射影定理的表达式及证明：如上图，Rt△ABF中，BD是斜边AF上的高。(1)AD/AB=AB/AF,AB²=AD.AF,由Rt△ADB∽Rt△ABF可证得；（2）DF/BF=BF/AF,BF²=DF.AF,由Rt△DFB∽Rt△BFA可证得；（3）DF/DB=DB/AD,DB=AD.DF,Rt△DFB∽Rt△DBA可证得。

目前初中数学教材里不提射影定理这个名称（就正如不提韦达定理一样），但是其所涉及的基本图形在习题和中考中却经常遇到，而且本身也不是知识难度拔高，所以掌握基本图形和结论，理解和消化结论的证明方法，并学会应用，无疑是很有必要的。

弦切角，是指顶点在圆上，一边和圆相交，另一边和圆相切的角。或者说，弦切角就是切线与含切点的弦所夹的角。

弦切角的性质: 弦切角等于同圆中它所夹的弧所对的圆周角。

例一

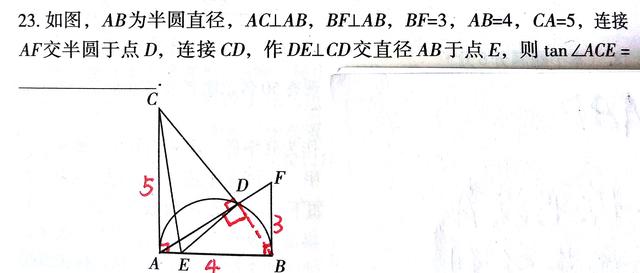
解答示范

提示：学生解题时，需要证明射影定理所引出的结论。

例二

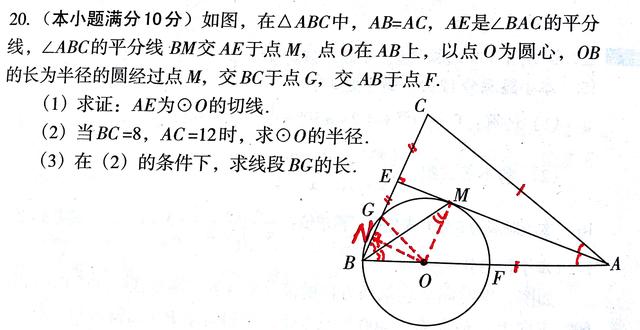
提示：本题第（3）小题灵活运用垂径定理是关键。学数学要得灵感，必须培养一种审题的眼力。