中考数学压轴题解析5：用分析法寻求思路突破，相似三角形为主干

方法科普

分析法，是指从要求解的问题出发，逐步寻求使它成立的充分条件，直到归结为显然成立的条件（已知量、定义、公理、定理、性质、法则等）为止，从而证明结论的正确性、合理性的一种论证方法。别名因果分析法、逆推法、执果索因法。

分析法，体现的数学思想是由果索因；运用思路是由未知探需知，逐步推向已知；适用范围是不易直接证明的问题。

下面这道中考题三个小题的解答，可以让同学们感受和学习 分析法的具体运用。

题目呈现

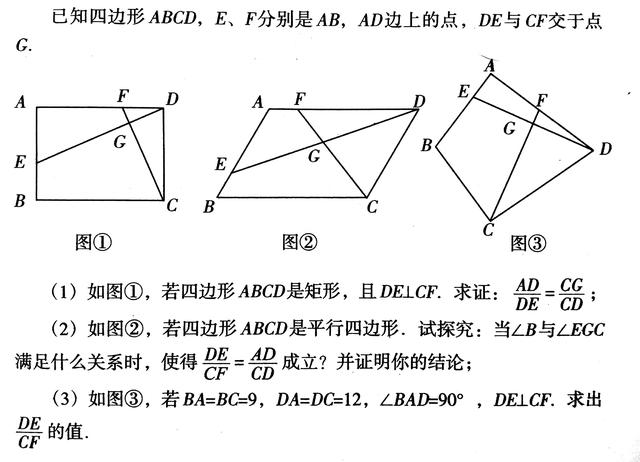
分析解答

第1小题：如图1.注意已知条件：四边形ABCD是矩形，且DE⊥CF。用分析法从结论入手逆推。AD/DE=CG/CD→△ADE∽△GCD→两组内角对应相等：∠A=∠DGC=90°，∠ADE=90°－-∠GDC=∠GCD。可证。反序写出过程即可。

第2小题：如图2.讨论对象由第1小题的矩形扩大为平行四边形,且不再有DE⊥CF的条件。第1小题中，直角三角形相似的共有：Rt△AED∽Rt△DFG∽Rt△FDC∽Rt△CGD。现在DE与CF不再垂直，那么相似的三角形组就减少了。但是仍然可以受此启发，寻求相似三角形组，反观对应角的关系。依然执果索因来逆推。显然△AED与△FDC不再相似，说明要证的比例线段只能靠第三方搭桥，即中间比转化。

AD/GD=DE/DF→△AED∽△GFD→∠GDF=∠ADE(已知的公共角），∠FGD(与∠EGC相关，且相等）=∠EAD。

GD/DF=CD/CF→△CGD∽△CDF→∠GCD=∠DCF(已知的公共角）,∠CGD(与∠EGC相关，且与之互补）=∠CDF。

而AD/GD=DE/DF即GD/DF=AD/DE,所以CD/CF=AD/DE,即题中结论DE/CF=AD/CD可以成立。而前提条件是：∠FGD=∠EAD，∠CGD=∠CDF。又因为∠FGD+∠CGD=180°，∠FGD=∠EGC，∠CDF=∠B，所以∠B+∠EGC=180°。也就是当这两个角满足互补关系时，DE/CF=AD/CD才成立。反序写出过程即可。

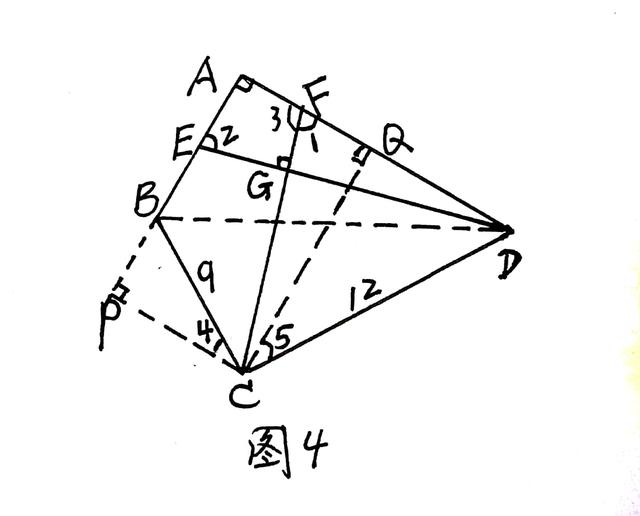
第3小题： 如图4. DE/CF→相似三角形组→∠1=∠2，直角一组→∠2+∠3=180°，过点C作CQ⊥AD于Q→∠A+∠EGF=180°（已知），∠A=∠FQC=Rt∠（已知及构造作图）。这个思路可行。为此，需求CQ（对应边AD=12已知）。

过点C作CP垂直于AB的延长线于P，则得矩形APCQ.于是AP=CQ，∠PCQ=90°。连接BD，则△ABD≌△CBD（SSS），∠BCD=90°。所以∠4=∠5=90°--∠BCQ。Rt△CPB∽Rt△CQD，得CP/CQ=CB/CD=9/12, CP=3/4CQ。PB=CQ--9。在Rt△PCB中，CP²+PB²=BC²，可得CQ=288/25.

最后，Rt△AED∽Rt△QFC, DE/CF=AD/CQ=12/（288/25）=25/24.

反思总结

分析法帮助寻求解题突破口，又常和综合法（由因到果）结合使用。这个特点在本题解答过程中体现十分鲜明。三角形相似的判定多次用到。三个小题的设置很有梯度，思维得到了很好的锻炼。