传说亚历山大城有一位精通数学和物理的学者,名叫海伦。一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题。将军每天从军营A出发,先到河边饮马,然后再去河岸同侧的B地开会,应该怎样走才能使路程最短?从此,这个被称为"将军饮马"的问题广泛流传。这个问题的解决并不难,据说海伦略加思索就解决了它。其实,解决这个问题的办法,就是利用轴对称思想。轴对称知识点使用,是求解线段和的最大值问题的常用方法,通常还涉及到利用三角形三边关系、两点之间线段最短、垂线段最短等相关知识点解决问题。常见的题型有:
1.已知:在直线l同恻有A.B两点,在l上找一点P,使得AP+PB最小;作法:如图.作点A关于直线l的对称点A’,连结A'B,与直线,的交点就是点P。
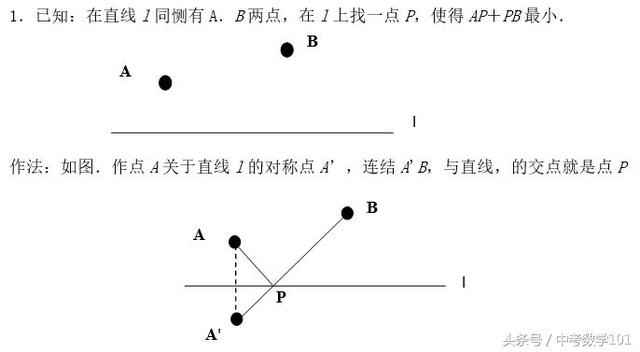
2.已知:在直线l同侧有A,B两点,在l上找一点P,使得|AP-PB|最小;作法:如图,连结AB,作线段AB的垂直平分线,与直线l的交点就是点P。
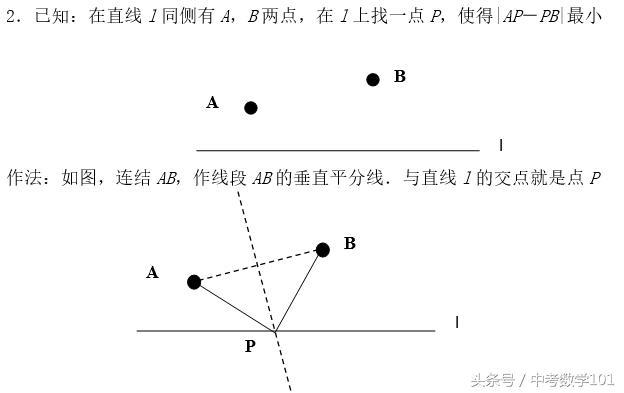
3.已知:在直线l同侧有A,B两点,在l上找一点P.使得|AP-PB|最大;作法:如图,连结BA并延长,与直线,的交点就是点P
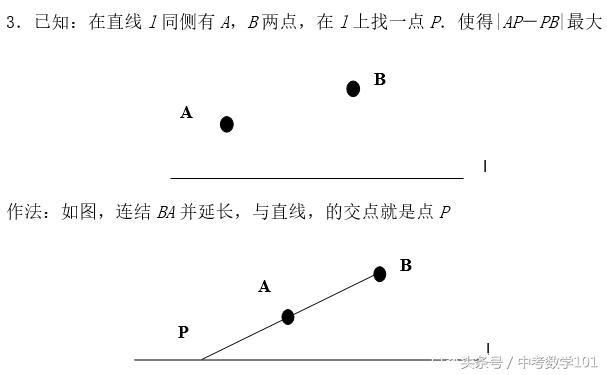
4.已知:在直线l同侧有A,B两点.在l上找两点C,D(其中CD的长度固定,等于所给线段a),使得AC+CD+DB最小;作法:如图,先将点A向右平移口个单位长度到点A',作A'关于直线l的对称点A",连结A"B,与直线l的交点就是点D.连结A'D,过点A作AC∥A'D,交直线l于点C.则此时AC'+CD+DB最小.
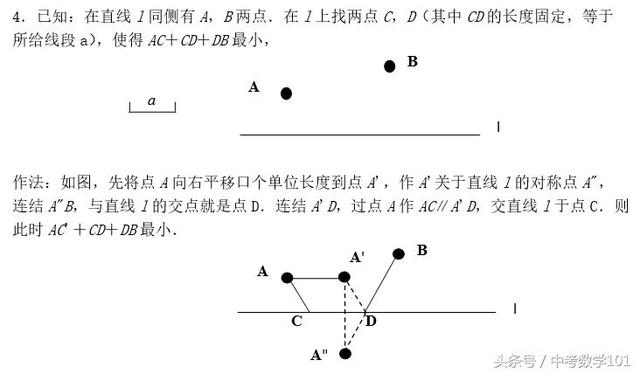
5.已知:在MON内有一点P,在边ON,OM上分别找点Q,R,使得PQ+QR+RP最小;作法:如图,分别作点P关于射线OM的对称点P',P",连结P'P",与射线ON,OM的交点就是点Q,R.
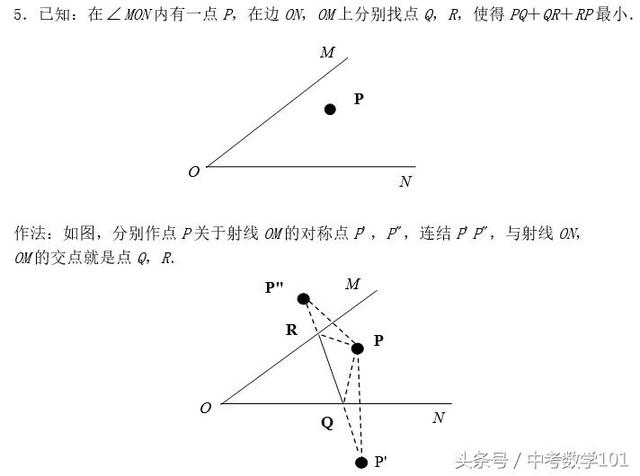
6.已知:在MON内有一点P,在边OM,ON上分别找点R,Q.使得PR+QR最小;作法:如图,作点P关于射线OM的对称点P',作P'QON,垂足为Q,P'Q与射线ON的交点就是R.
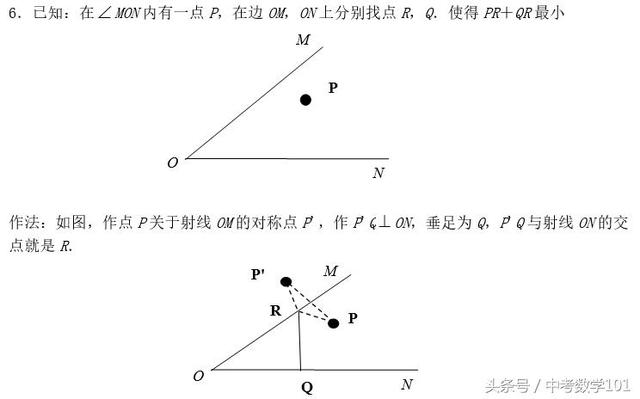
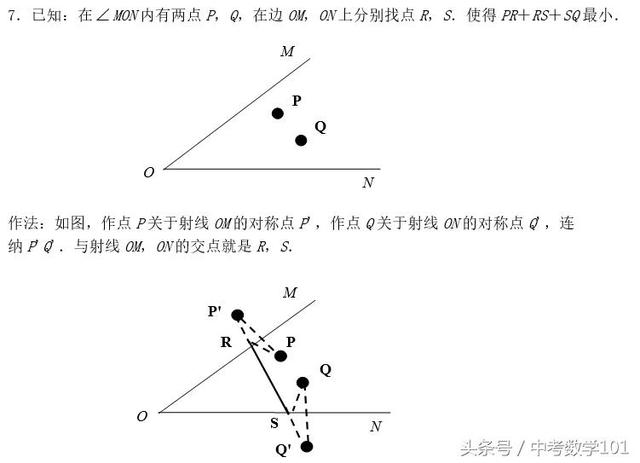
7.已知:在MON内有两点P,Q,在边OM,ON上分别找点R,S.使得PR+RS+SQ最小;作法:如图,作点P关于射线OM的对称点P',作点Q关于射线ON的对称点Q',连接P'Q'.与射线OM,ON的交点就是R,S.
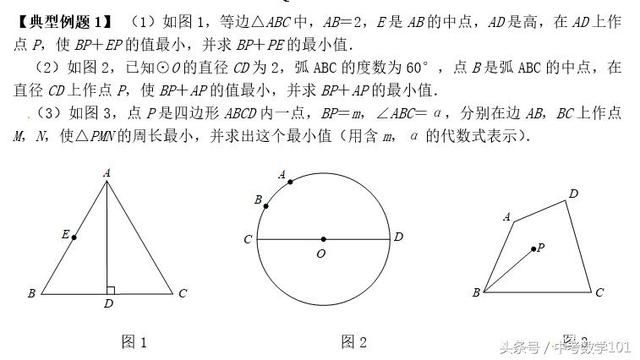

 加载中,请稍侯......
加载中,请稍侯......
精彩评论